

分析 首先从多面体外形入手,外形都是正方形,说明多面体是由一个正方体切割而成.结合多面体从前面、后面、左侧、右侧、上方视图,发现该多面体是由一个正方体沿着相邻三个面的对角线切割去一个三棱锥.其体积等于正方体体积减去三棱锥体积.其表面积是:三个面的平面成了三角形,多了一个等边三角形的平面.
解答 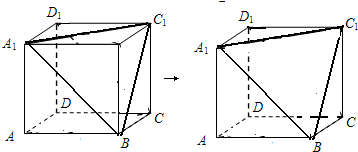
解:该多面体是由一个正方体沿着相邻三个面的对角线切割去一个三棱锥.
∴其体积:V=V正-V锥
$V=1×1×1-\frac{1}{3}×1×1×\frac{1}{2}×1$
V=$\frac{5}{6}$;
其表面积:
S表=3S正方形+3S三角形+S等边三角形
=$3×1×1+3×1×1×\frac{1}{2}+\frac{1}{2}×\sqrt{2}×\frac{\sqrt{6}}{2}$
=$\frac{9}{2}+\frac{\sqrt{3}}{2}$
=$\frac{9+\sqrt{3}}{2}$
故填:$\frac{5}{6}$,$\frac{9+\sqrt{3}}{2}$.
点评 本题考查了多面体的视图判断多面体的形状,求其体积和表面积,多采用“补形还原法,或者分割法”,还原成熟悉的立体图或者分割成熟悉的正方体或长方体或者棱柱棱锥.注重对空间思维的培养和开发.属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,-$\frac{1}{3}}$] | B. | [-$\frac{1}{2}$,-$\frac{1}{3}}$] | C. | [-3,-2] | D. | (-3,-2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
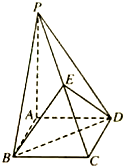 如图,四边形ABCD为菱形,∠ABC=60°,PA⊥平面ABCD,E为PC的中点.
如图,四边形ABCD为菱形,∠ABC=60°,PA⊥平面ABCD,E为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | 9 | D. | 36 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com