
| A. | (-$\frac{1}{2}$,-$\frac{1}{3}}$] | B. | [-$\frac{1}{2}$,-$\frac{1}{3}}$] | C. | [-3,-2] | D. | (-3,-2] |
分析 讨论方程类型和方程在(0,3]上的根的个数,利用二次函数的性质列出不等式解出.
解答 解:当a=0时,方程x+1=0的零点为-1,不符合题意,∴a≠0.
(1)若方程在(0,3]有一个根,
①若3为方程的根,则12a+4=0,解得a=-$\frac{1}{3}$,
②若3不是方程的根,则$\left\{\begin{array}{l}{△=1-4a(3a+1)=0}\\{0<-\frac{1}{2a}<3}\end{array}\right.$或$\left\{\begin{array}{l}{△=1-4a(3a+1)>0}\\{(3a+1)(12a+4)<0}\end{array}\right.$.
解得a=-$\frac{1}{2}$或无解.
(2)若方程在(0,3]上有两个根,则$\left\{\begin{array}{l}{△-1-4a(3a+1)>0}\\{0<-\frac{1}{2a}<3}\\{3a+1<0}\\{12a+4≤0}\\{a<0}\end{array}\right.$,
解得:-$\frac{1}{2}$<x≤-$\frac{1}{3}$,
综上,a的范围是[-$\frac{1}{2}$,-$\frac{1}{3}$].
故选B.
点评 本题考查了方程根的个数判断,一元二次方程与二次函数的关系,不等式的解法,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
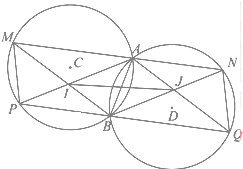 如图,圆C与圆D半径分别为r1,r2,相交于A,B两点,直线l1过点A,分别交圆C、圆D于点M、N(M、N在A的异侧),直线l2过点B,分别交圆C、圆D于点P,Q(P、Q在B的异侧),且l1平行于
如图,圆C与圆D半径分别为r1,r2,相交于A,B两点,直线l1过点A,分别交圆C、圆D于点M、N(M、N在A的异侧),直线l2过点B,分别交圆C、圆D于点P,Q(P、Q在B的异侧),且l1平行于查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com