
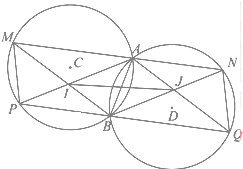
 如图,圆C与圆D半径分别为r1,r2,相交于A,B两点,直线l1过点A,分别交圆C、圆D于点M、N(M、N在A的异侧),直线l2过点B,分别交圆C、圆D于点P,Q(P、Q在B的异侧),且l1平行于
如图,圆C与圆D半径分别为r1,r2,相交于A,B两点,直线l1过点A,分别交圆C、圆D于点M、N(M、N在A的异侧),直线l2过点B,分别交圆C、圆D于点P,Q(P、Q在B的异侧),且l1平行于分析 (1)证明两组对边分别平行,即可证明四边形MNQP为平行四边形;
(2)证明MB∥AQ,PA∥BN,可得四边形AIBJ为平行四边形,即可证明:线段AB与线段IJ互相平分.
解答 证明:(1)由题意可知四边形MABP,NABQ均为等腰梯形,
∴∠PMA=∠ABQ=∠BQN,
∴∠PMA+∠ANQ=∠BQN+∠ANQ=180°,
∴PM∥QN,
又∵MN∥PQ,
∴四边形MNQP是平行四边形;
(2)∵SMABP=SNABQ,
∴PB+MA=BQ+AN,
又∵MN=PQ,
∴MA=BQ,MA∥BQ,
∴四边形MAQB为平行四边形,
∴MB∥AQ,同理可得PA∥BN,
∴四边形AIBJ为平行四边形,
∴线段AB与线段IJ互相平分.
点评 本题考查平行四边形的证明,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 720 | B. | 840 | C. | 960 | D. | 1080 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥0} | B. | {x|x<1} | C. | {x|0≤x<1} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,-$\frac{1}{3}}$] | B. | [-$\frac{1}{2}$,-$\frac{1}{3}}$] | C. | [-3,-2] | D. | (-3,-2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知A,B,C,D为圆O上的四点,直线PA切圆O于点A,PA∥BD,AC与BD相交于G点.
已知A,B,C,D为圆O上的四点,直线PA切圆O于点A,PA∥BD,AC与BD相交于G点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
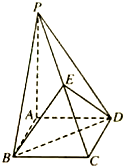 如图,四边形ABCD为菱形,∠ABC=60°,PA⊥平面ABCD,E为PC的中点.
如图,四边形ABCD为菱形,∠ABC=60°,PA⊥平面ABCD,E为PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com