
分析 (1)利用已知条件判断复数z1的轨迹;(2)利用复数的乘法的几何意义,求出∠AOB,表示出三角形的面积,然后求解最值即可.
解答 解:在复平面内,△AOB中,O是原点,点A,B对应的复数分别为z1,z2,且z1,z2满足以下条件:
(1)|z1-3|=1,可得复数z1是复平面,以(3,0)为圆心,以1为半径的圆.|z1|的最小值为:2,最大值为:4.
(2)z2=(-1+i)z1=$\sqrt{2}$(cos$\frac{3π}{4}$+isin$\frac{3π}{4}$)z1,可知$\overrightarrow{O{Z}_{1}}$与$\overrightarrow{O{Z}_{2}}$的夹角为:$\frac{3π}{4}$,即:∠AOB=$\frac{3π}{4}$.
△AOB面积为:$\frac{1}{2}$|z1||z2|sin$\frac{3π}{4}$=$\frac{\sqrt{2}}{2}$|z1|2×$\frac{\sqrt{2}}{2}$=$\frac{1}{2}$|z1|2∈[2,8]
可得△AOB面积的最大值和最小值分别为:8,2.
点评 本题考查复数的几何意义,轨迹方程的应用,考查转化思想以及计算能力.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:解答题
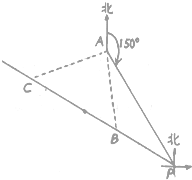 海滨某城市A附近海面上有一台风,在城市A测得该台风中心位于方位角150°、距离400km的海面P处,并正以70km/h的速度沿北偏西60°的方向移动,如果台风侵袭的范围是半径为250km的圆形区域.
海滨某城市A附近海面上有一台风,在城市A测得该台风中心位于方位角150°、距离400km的海面P处,并正以70km/h的速度沿北偏西60°的方向移动,如果台风侵袭的范围是半径为250km的圆形区域.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com