
分析 (1)当n=1时,a1=1,当n≥2时,Sn-1+an-1=2(n-1),与原式相减,2an=an-1+2,即2(an-2)=an-1-2,a1-2=-1,数列{an-2}是以-1为首项,$\frac{1}{2}$为公比的等比数列;
(2)由(1)可知,an-2=-($\frac{1}{2}$)n-1,代入即可求得Sn=2n-an=2n-2+($\frac{1}{2}$)n-1,根据等比数列及等差数列前n项和公式,即可求得数列{Sn}的前n项和Tn.
解答 解:(1)证明:当n=1时,S1+a1=2,即a1=1,
∵Sn+an=2n①,
当n≥2时,Sn-1+an-1=2(n-1)②,
由①-②得,2an-an-1=2,
∴2an=an-1+2,
∴2(an-2)=an-1-2,
∵a1-2=-1,
∴数列{an-2}是以-1为首项,$\frac{1}{2}$为公比的等比数列;
(2)解:由(1)得an-2=-($\frac{1}{2}$)n-1,
∴an=2-($\frac{1}{2}$)n-1,
∵Sn+an=2n,
∴Sn=2n-an=2n-2+($\frac{1}{2}$)n-1,
∴Tn=[0+($\frac{1}{2}$)0]+[2+($\frac{1}{2}$)1]+…+[2n-2+($\frac{1}{2}$)n-1],
=[0+2+4+…+(2n-2)]+[1+$\frac{1}{2}$+$\frac{1}{4}$+…+($\frac{1}{2}$)n-1],
=$\frac{n(2n-2)}{2}$+$\frac{1-({\frac{1}{2})}^{n}}{1-\frac{1}{2}}$,
=n2-n-2-($\frac{1}{2}$)n-1.
∴数列{Sn}的前n项和Tn=n2-n-2-($\frac{1}{2}$)n-1.
点评 本题考查等比数列通项公式,考查等比数列和等差数列前n项和公式,考查计算能力,属于中档题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | 720 | B. | 840 | C. | 960 | D. | 1080 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
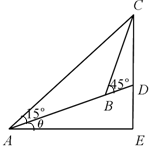 如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测得斜度为45°,建筑物的高CD为50米.
如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测得斜度为45°,建筑物的高CD为50米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥0} | B. | {x|x<1} | C. | {x|0≤x<1} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
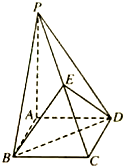 如图,四边形ABCD为菱形,∠ABC=60°,PA⊥平面ABCD,E为PC的中点.
如图,四边形ABCD为菱形,∠ABC=60°,PA⊥平面ABCD,E为PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com