
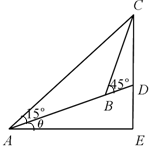
 如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测得斜度为45°,建筑物的高CD为50米.
如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测得斜度为45°,建筑物的高CD为50米.分析 (1)在三角形ABC中,由∠CBD-∠CAB求出∠ACB的度数,再由AB的长,以及sin∠CAB与sin∠ACB的值,利用正弦定理表示出BC;
(2)在三角形DBC中,由CD,∠CBD=45°与∠CDB=90°+θ,利用正弦定理列出关系式,将各自的值代入利用诱导公式化简,即可求出cosθ的值.
解答 解:(1)在△ABC中,∠BAC=15°,AB=100米,∠ACB=45°-15°=30°.
根据正弦定理有$\frac{100}{sin30°}$=$\frac{BC}{sin15°}$,∴BC=50($\sqrt{6}$-$\sqrt{2}$).…(6分)
(2)在△BCD中,∵CD=50,BC=$\frac{100sin15°}{sin30°}$,∠CBD=45°,∠CDB=90°+θ,
根据正弦定理有$\frac{CD}{sin45°}$=$\frac{BC}{sin(90°+θ)}$,
解得cosθ=$\sqrt{3}$-1 …(12分)
点评 此题考查了正弦定理,两角和与差的正弦函数公式,诱导公式,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:解答题
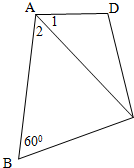 如图,在四边形ABCD中,∠1=∠2,∠ABC=60°,AC=7,AD=6,S△ADC=$\frac{{15\sqrt{3}}}{2}$
如图,在四边形ABCD中,∠1=∠2,∠ABC=60°,AC=7,AD=6,S△ADC=$\frac{{15\sqrt{3}}}{2}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
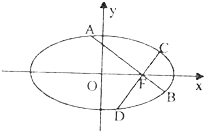 设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,右焦点F为抛物线y2=4x的焦点.
设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,右焦点F为抛物线y2=4x的焦点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 个人家庭用车消费汽油费 | ≤880元/月 | 880~920元/月 | 920~940元/月 | ≥940元/月 |
| 税 率 | 不纳税 | 0.01 | 0.02 | 0.05 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{15}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,+∞) | B. | [4,+∞) | C. | (-∞,4) | D. | (-∞,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{{\sqrt{21}}}$ | B. | $\frac{3}{{\sqrt{21}}}$ | C. | $\frac{4}{{\sqrt{21}}}$ | D. | $\frac{5}{{\sqrt{21}}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com