
| A. | $\frac{{\sqrt{15}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
分析 设BM=1,AC=h,利用两角和差的正切公式计算tan∠BAM,列出方程解出AC,即可求出AB,得出sin∠BAC.
解答 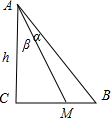 解:设∠BAM=α,∠CAM=β,BC=3BM=3,AC=h.
解:设∠BAM=α,∠CAM=β,BC=3BM=3,AC=h.
则tanβ=$\frac{2}{h}$,tan(α+β)=$\frac{3}{h}$,
∴tanα=$\frac{\frac{3}{h}-\frac{2}{h}}{1+\frac{6}{{h}^{2}}}$=$\frac{h}{{h}^{2}+6}$.
又sinα=$\frac{1}{5}$,∴cosα=$\frac{2\sqrt{6}}{5}$,∴tanα=$\frac{1}{2\sqrt{6}}$.
∴$\frac{h}{{h}^{2}+6}=\frac{1}{2\sqrt{6}}$,解得h=$\sqrt{6}$.
∴AB=$\sqrt{{h}^{2}+9}$=$\sqrt{15}$.
∴sin∠BAC=$\frac{BC}{AB}$=$\frac{3}{\sqrt{15}}$=$\frac{\sqrt{15}}{5}$.
故选:A.
点评 本题考查了三角形中的几何运算,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{1}{3}})$ | B. | $[{-\frac{1}{3},+∞})$ | C. | $({-\frac{1}{3},+∞})$ | D. | $({-∞,-\frac{1}{3}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
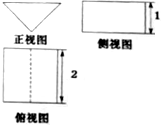 《九章算术》中,将底面是直角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,俯视图中虚线平分矩形的面积,则该“堑堵”的表面积为( )
《九章算术》中,将底面是直角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,俯视图中虚线平分矩形的面积,则该“堑堵”的表面积为( )| A. | 4+2$\sqrt{2}$ | B. | 2 | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
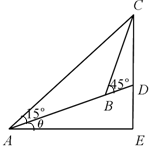 如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测得斜度为45°,建筑物的高CD为50米.
如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测得斜度为45°,建筑物的高CD为50米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com