
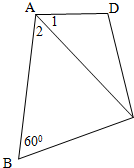
 如图,在四边形ABCD中,∠1=∠2,∠ABC=60°,AC=7,AD=6,S△ADC=$\frac{{15\sqrt{3}}}{2}$
如图,在四边形ABCD中,∠1=∠2,∠ABC=60°,AC=7,AD=6,S△ADC=$\frac{{15\sqrt{3}}}{2}$分析 (Ⅰ)利用三角形的面积公式求出sin∠1的值,再利用同角的三角函数关系求出cos∠1,用余弦定理即可求出DC的长;
(Ⅱ)根据∠1=∠2求出∠2的正弦、余弦值,再利用三角形内角和定理与三角恒等变换即可求出sin∠BCA的值.
解答 解:(Ⅰ)△ADC中,AC=7,AD=6,S△ADC=$\frac{15\sqrt{3}}{2}$,
即S△ADC=$\frac{1}{2}$•AC•AD•sin∠1=$\frac{1}{2}$×7×6×sin∠1=$\frac{15\sqrt{3}}{2}$,
∴sin∠1=$\frac{5\sqrt{3}}{14}$,
∴cos∠1=$\sqrt{1{-(\frac{5\sqrt{3}}{14})}^{2}}$=$\frac{11}{14}$
∴DC2=AC2+AD2-2•AC•AD•cos∠1
=72+62-2×7×6×$\frac{11}{14}$
=19,
∴DC=$\sqrt{19}$;
(Ⅱ)∵∠1=∠2,
∴sin∠2=sin∠1=$\frac{5\sqrt{3}}{14}$,cos∠2=cos∠1=$\frac{11}{14}$;
又∠ABC=60°,
∴sin∠BCA=sin(120°-∠2)
=sin120°cos∠2-cos120°sin∠1
=$\frac{\sqrt{3}}{2}$×$\frac{11}{14}$-(-$\frac{1}{2}$)×$\frac{5\sqrt{3}}{14}$
=$\frac{4\sqrt{3}}{7}$.
点评 本题考查了余弦定理,三角形的面积公式,三角形的内角和定理,以及两角差的正弦公式,熟练掌握定理及公式是解题的关键,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | i | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{13}+2$ | B. | $\sqrt{13}-2$ | C. | $\sqrt{13}+1$ | D. | $\sqrt{13}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{1}{3}})$ | B. | $[{-\frac{1}{3},+∞})$ | C. | $({-\frac{1}{3},+∞})$ | D. | $({-∞,-\frac{1}{3}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知定义在(0,+∞)上的函数f(x)=2x+$\frac{10}{x}$.设点P是函数图象上的任意一点,过点P分别作直线y=2x和y轴的垂线,垂足分别为M、N.
已知定义在(0,+∞)上的函数f(x)=2x+$\frac{10}{x}$.设点P是函数图象上的任意一点,过点P分别作直线y=2x和y轴的垂线,垂足分别为M、N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
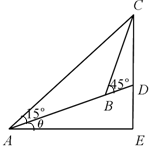 如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测得斜度为45°,建筑物的高CD为50米.
如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测得斜度为45°,建筑物的高CD为50米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com