
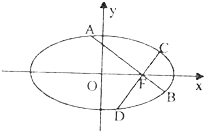
 设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,右焦点F为抛物线y2=4x的焦点.
设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,右焦点F为抛物线y2=4x的焦点.分析 (1)由题意:离心率为$\frac{1}{2}$,右焦点F为抛物线y2=4x的焦点.建立关系解出a,b.
(2)①:利用F,设其中一条直线方程,设而不求法;把AB和CD线段表示出来,圆锥曲线的定义、性质与方程求证即可.
②直线l1,l2相互垂直,利用①,即可求四边形ACBD面积的最大值和最小值.
解答 解:(1)由题意:离心率为$\frac{1}{2}$,右焦点F为抛物线y2=4x的焦点.
∴e=$\frac{c}{a}=\frac{1}{2}$,右焦点F(c,0),抛物线y2=4x的焦点为:(1,0)
∴c=1,a=2,b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{3}$
所以:椭圆C的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)由(1)可知右焦点F(1,0),
k不存在时:过AB直线l1为:x=1,则过CD直线l2为:y=0
∴|AB|=3,|CD|=2a=4
所以:$\frac{1}{|AB|}$+$\frac{1}{|CD|}$=$\frac{1}{4}+\frac{1}{3}=\frac{7}{12}$(定值)
k存在时:
设过AB直线l1为:y=k(x-1),则过CD直线l2为:y=$-\frac{1}{k}$(x-1),
设A(xA,yA),B((xB,yB))C(xC,yC),D(xD,yD)
由$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,y=k(x-1),
可得:xA+xB=$\frac{8{k}^{2}}{3+4{k}^{2}}$
xAxB=$\frac{4{k}^{2}-12}{3+4{k}^{2}}$
|AB|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{A}-{x}_{B})^{2}-4{x}_{A}{x}_{B}}$=$\frac{12(1+{k}^{2})}{3+4{k}^{2}}$
同理:
由$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,y=$-\frac{1}{k}$(x-1),
可得:xC+xD=$\frac{8}{3{k}^{2}+4}$
xCxD=$\frac{4-12{k}^{2}}{3{k}^{2}+4}$
|CD|=$\frac{12({k}^{2}+1)}{4+3{k}^{2}}$
∴$\frac{1}{|AB|}$+$\frac{1}{|CD|}$=$\frac{7}{12}$(定值)
②四边形ACBD面积=|AB|×|CD|
当k不存在时:|AB|=$\frac{2{b}^{2}}{a}$=3,|CD|=2a=4
S=$\frac{1}{2}$×3×4=6
k存在时:
S=$\frac{1}{2}×$$\frac{12(1+{k}^{2})}{3+4{k}^{2}}$×$\frac{12({k}^{2}+1)}{4+3{k}^{2}}$=$\frac{72({k}^{2}+1)^{2}}{12{k}^{4}+25{k}^{2}+12}$=$\frac{72({k}^{2}+1)^{2}}{12({k}^{2}+1)^{2}+{k}^{2}}$=$\frac{72}{12+(\frac{k}{{k}^{2}+1})^{2}}$
令$y=\frac{k}{{k}^{2}+1}$
则$\frac{1}{y}=k+\frac{1}{k}≥2$(当且当k=1时取等号)
∴$0≤{y}^{2}≤\frac{1}{4}$
所以:Smax=6
${S}_{min}=\frac{288}{49}$
点评 本题考查了直线与圆锥曲线位置关系的应用,考查了椭圆的简单性质,考查弦长公式的应用,体现了“设而不求”的解题思想方法,基本不等式的运用,计算量大,要求能力高,属于难题.


科目:高中数学 来源: 题型:解答题
 已知定义在(0,+∞)上的函数f(x)=2x+$\frac{10}{x}$.设点P是函数图象上的任意一点,过点P分别作直线y=2x和y轴的垂线,垂足分别为M、N.
已知定义在(0,+∞)上的函数f(x)=2x+$\frac{10}{x}$.设点P是函数图象上的任意一点,过点P分别作直线y=2x和y轴的垂线,垂足分别为M、N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 720 | B. | 840 | C. | 960 | D. | 1080 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
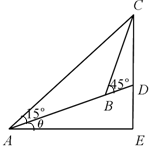 如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测得斜度为45°,建筑物的高CD为50米.
如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测得斜度为45°,建筑物的高CD为50米.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com