已知函数
（1）当函数
取得最大值时，求自变量
的集合；
（2）该函数的图象可由
的图象经过怎样的平移和伸缩变换得到？
（1）当y取得最大值时，x的集合为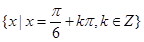
，（2）略.
解析试题分析：（1）欲求函数最值，需将函数化为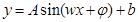
的形式,首先应将三角函数的次数化为一次，利用
,
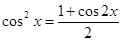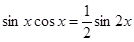,代入并配角合并；（2）函数的平移要注意方向和平移的量，并注意平移是针对变量而言的，伸缩也是针对变量而言，即在变量上变化.
试题解析：
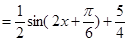2分
当y取得最大值时，必需且只需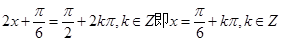
当y取得最大值时，x的集合为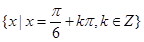 6分
（2）将函数y=sinx的图象依次进行如下变换：
1）把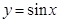
的图象向左平移
，得
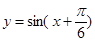图象.
2）把所得图象上的各点横坐标缩到原来的
（纵坐标不变）
得到函数
的图象 10分
3）把所得图象上的各点纵坐标缩到原来的（横坐标不变）
得到函数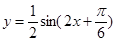
的图象
4）把图象上移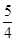
个大内长度，得
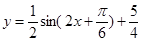图象
综上得到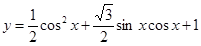
的图象 14分
考点：（1）三角函数最值；（2）三角函数平移和伸缩变化.
新非凡教辅冲刺100分系列答案科目：高中数学 来源： 题型：解答题
已知A(x1,f(x1))，B(x2,f(x2))是函数f(x)=2sin(wx+j)(w＞0,
＜j＜0)图象上的任意两点，且角j的终边经过点P(l，-
)，若|f(x1)-f(x2)|=4时，|x1-x2|的最小值为
.
(1)求函数f(x)的解析式；(2)求函数f(x)的单调递增区间；(3)当x∈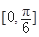
时，不等式mf(x)+2m≥f(x)恒成立，求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，α为第三象限角．
，
的值；
），tan2α的值．
.
的最小正周期；
，
，若函数
.
，求
值；
，求
中，内角
所对边长分别为
，
，
．
的最大值及
的取值范围；
的值域．
平移后，得到的图象的表达式为
，则原函数的解析式为 
．若
是奇函数，则
__________．
，若
，
则x的取值范围为