
 、
、 、
、 、
、 满足:
满足: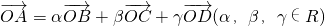 ,B、C、D为不共线三点,给出下列命题:
,B、C、D为不共线三点,给出下列命题: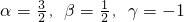 ,则A、B、C、D四点在同一平面上;
,则A、B、C、D四点在同一平面上;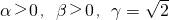 时,若
时,若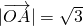 ,
,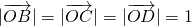 ,
,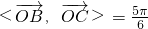 ,
,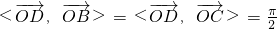 ,则α+β的最大值为
,则α+β的最大值为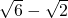 ;
;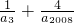 的最小值为9;
的最小值为9; 所成的比λ一定为
所成的比λ一定为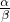 .
.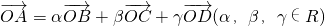 且α+β+γ=1,则A、B、C、D四点在同一平面上;可知①正确;②把
且α+β+γ=1,则A、B、C、D四点在同一平面上;可知①正确;②把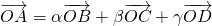 两边平方,化成3=α2
两边平方,化成3=α2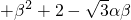 ,即=(α+β)2-(2
,即=(α+β)2-(2 )αβ+2,利用基本不等式即可求得α+β的最大值为4+2
)αβ+2,利用基本不等式即可求得α+β的最大值为4+2 ,,故可知②错;③根据α=a2,β=a2009,γ=0,且A、B、C三点共线,可得a2+a2009=1,利用等差数列的性质可得a3+a2008=1,利用基本不等式即可求得结果;④根据三点共线的充要条件可知
,,故可知②错;③根据α=a2,β=a2009,γ=0,且A、B、C三点共线,可得a2+a2009=1,利用等差数列的性质可得a3+a2008=1,利用基本不等式即可求得结果;④根据三点共线的充要条件可知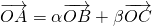 且α+β=1,则A、B、C三点共线,而A分
且α+β=1,则A、B、C三点共线,而A分 所成的比λ一定为
所成的比λ一定为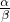 错,如点A在线段BC的延长线上,且BA=
错,如点A在线段BC的延长线上,且BA= ,λ=-3,而此时的
,λ=-3,而此时的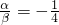 ,因此错.
,因此错.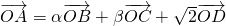 ,两边平方得,3=α2
,两边平方得,3=α2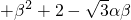
 )αβ+2≥(α+β)2-(2
)αβ+2≥(α+β)2-(2 )
)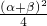 +2,
+2, ,当且仅当
,当且仅当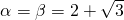 时等号成立,故②错;
时等号成立,故②错;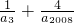 =(
=(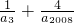 )(a3+a2008)≥5+4=9.③对.
)(a3+a2008)≥5+4=9.③对. ,λ=-3,
,λ=-3,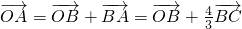
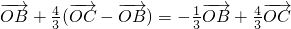 ,
,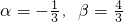 ,∴
,∴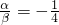 ,
,

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com