
【题目】已知△ABC的三边BC,CA,AB的中点分别是D(5,3),E(4,2),F(1,1).
(1)求△ABC的边AB所在直线的方程及点A的坐标;
(2)求△ABC的外接圆的方程.
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】为庆祝党的98岁生日,某高校组织了“歌颂祖国,紧跟党走”为主题的党史知识竞赛。从参加竞赛的学生中,随机抽取40名学生,将其成绩分为六段![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,到如图所示的频率分布直方图.
,到如图所示的频率分布直方图.

(1)求图中![]() 的值及样本的中位数与众数;
的值及样本的中位数与众数;
(2)若从竞赛成绩在![]() 与
与![]() 两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于
两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于![]() 分为事件
分为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过直线2x+y+4=0和圆x2+y2+2x﹣4y+1=0的交点,且面积最小的圆方程为( )
A.(x+![]() )2+(y+
)2+(y+![]() )2=
)2=![]() B.(x﹣
B.(x﹣![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
C.(x﹣![]() )2+(y+
)2+(y+![]() )2=
)2=![]() D.(x+
D.(x+![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】坐标系与参数方程在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,直线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ).
).
(1)写出直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)平移直线![]() 使其经过曲线
使其经过曲线![]() 的焦点,求平移后的直线的极坐标方程.
的焦点,求平移后的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过直线2x+y+4=0和圆x2+y2+2x﹣4y+1=0的交点,且面积最小的圆方程为( )
A.(x+![]() )2+(y+
)2+(y+![]() )2=
)2=![]() B.(x﹣
B.(x﹣![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
C.(x﹣![]() )2+(y+
)2+(y+![]() )2=
)2=![]() D.(x+
D.(x+![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省确定从2021年开始,高考采用“![]() ”的模式,取消文理分科,即“3”包括语文、数学、英语,为必考科目:“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取
”的模式,取消文理分科,即“3”包括语文、数学、英语,为必考科目:“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取![]() 名学生进行调查.
名学生进行调查.
(1)已知抽取的![]() 名学生中含男生110人,求
名学生中含男生110人,求![]() 的值及抽取到的女生人数;
的值及抽取到的女生人数;
(2)学校计划在高二上学期开设选修中的“物理”和“历史”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的![]() 名学生讲行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目).下表是根据调查结果得到的
名学生讲行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目).下表是根据调查结果得到的![]() 列联表,请将列联表补充完整,并判断是否有
列联表,请将列联表补充完整,并判断是否有![]() 的把握认为选择科目与性别有关?说明你的理由;
的把握认为选择科目与性别有关?说明你的理由;
性别 | 选择物理 | 选择历史 | 总计 |
男生 | 50 | ||
女生 | 30 | ||
总计 |
(3)在(2)的条件下,从抽取的选择“物理”的学生中按分层抽样抽取6人,再从这6名学生中抽取2人,对“物理”的选课意向作深入了解,求2人中至少有1名女生的概率.
参考公式:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
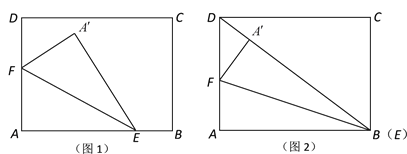
【题目】南通风筝是江苏传统手工艺品之一.现用一张长2 m,宽1.5 m的长方形牛皮纸ABCD裁剪风筝面,裁剪方法如下:分别在边AB,AD上取点E,F,将三角形AEF沿直线EF翻折到![]() 处,点
处,点![]() 落在牛皮纸上,沿
落在牛皮纸上,沿![]() ,
,![]() 裁剪并展开,得到风筝面
裁剪并展开,得到风筝面![]() ,如图1.
,如图1.
(1)若点E恰好与点B重合,且点![]() 在BD上,如图2,求风筝面
在BD上,如图2,求风筝面![]() 的面积;
的面积;
(2)当风筝面![]() 的面积为
的面积为![]() 时,求点
时,求点![]() 到AB距离的最大值.
到AB距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com