
【题目】随着南宁三中集团化发展,南宁三中青三校区2018年被清华北大录取23人,广西领先,一本率连年攀升,南宁三中青山校区2014年至2018年一本率如下表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
时间代号 | 1 | 2 | 3 | 4 | 5 |
一本率 | 0.7152 | 0.7605 | 0.7760 | 0.8517 | 0.9015 |
(1)求![]() 关于
关于![]() 的回归方程
的回归方程![]() (精确到0.0001);
(精确到0.0001);
(2)用所求回归方程预测南宁三中青山校区2019年高考一本录取率.(精确到0.0001).
附:回归方程![]() 中
中
参考数据:![]()
科目:高中数学 来源: 题型:
【题目】某厂拟生产甲、乙两种适销产品,每件销售收入分别为3000元,2000元.甲、乙产品都需要在A、B两种设备上加工,在每台A、B设备上加工一件甲所需工时分别为1![]() ,2
,2![]() ,加工一件乙设备所需工时分别为2
,加工一件乙设备所需工时分别为2![]() ,1
,1![]() .A、B两种设备每月有效使用台时数分别为400
.A、B两种设备每月有效使用台时数分别为400![]() 和500
和500![]() ,分别用
,分别用![]() 表示计划每月生产甲,乙产品的件数.
表示计划每月生产甲,乙产品的件数.
(Ⅰ)用![]() 列出满足生产条件的数学关系式,并画出相应的平面区域;
列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问分别生产甲、乙两种产品各多少件,可使收入最大?并求出最大收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点F1、F2是椭圆C1的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2 , 椭圆C1与双曲线C2的离心率分别为e1、e2 , 则( ) 
A.e22= ![]()
B.e22= ![]()
C.e22= ![]()
D.e22= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,已知曲线C的极坐标方程为![]() ,它在点
,它在点![]() 处的切线为直线l.
处的切线为直线l.
(1)求直线l的直角坐标方程;
(2)设直线l与![]() 的交点为P1,P2,求过线段P1P2的中点且与l垂直的直线的极坐标方程.
的交点为P1,P2,求过线段P1P2的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机给人们的生活带来便利的同时,也给青少年的成长带来不利的影响,有人沉迷于手机游戏无法自拔,严重影响了自己的学业,某学校随机抽取![]() 个班,调查各班带手机来学校的人数,所得数据的茎叶图如图所示.以组距为
个班,调查各班带手机来学校的人数,所得数据的茎叶图如图所示.以组距为![]() 将数据分组成
将数据分组成![]() ,
,![]() ,…,
,…,![]() ,
,![]() 时,所作的频率分布直方图是( )
时,所作的频率分布直方图是( )

A.  B.
B. 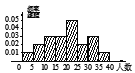
C. 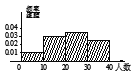 D.
D. 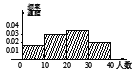
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题:
(1)“若![]() ,则
,则![]() ,
,![]() 互为倒数”的逆命题;
互为倒数”的逆命题;
(2)“面积相等的三角形全等”的否命题;
(3)“若![]() ,则
,则![]() 有实数解”的逆否命题;
有实数解”的逆否命题;
(4)“若![]() ,则
,则![]() ”的逆否命题.
”的逆否命题.
其中真命题为( )
A. (1)(2) B. (2)(3) C. (4) D. (1)(2)(3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 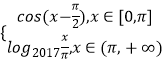 ,若有三个不同的实数a,b,c,使得f(a)=f(b)=f(c),则a+b+c的取值范围为( )
,若有三个不同的实数a,b,c,使得f(a)=f(b)=f(c),则a+b+c的取值范围为( )
A.(2π,2017π)
B.(2π,2018π)
C.( ![]() ,
, ![]() )
)
D.(π,2017π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2.
(Ⅰ)求证:CE∥平面PAD;
(Ⅱ)求PD与平面PCE所成角的正弦值;
(Ⅲ)在棱AB上是否存在一点F,使得平面DEF⊥平面PCE?如果存在,求 ![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等差数列,数列{bn}是等比数列,Sn是数列{an}的前n项和,a1=b1=1,S2=![]() .
.
(1)若b2是a1,a3的等差中项,求数列{an}与{bn}的通项公式;
(2)若an∈N+,数列{![]() }是公比为9的等比数列,求证:
}是公比为9的等比数列,求证:![]() +
+![]() +
+![]() +…+
+…+![]() <
<![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com