
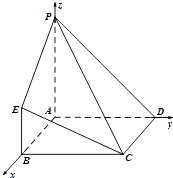
【题目】在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2.
(Ⅰ)求证:CE∥平面PAD;
(Ⅱ)求PD与平面PCE所成角的正弦值;
(Ⅲ)在棱AB上是否存在一点F,使得平面DEF⊥平面PCE?如果存在,求 ![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
【答案】解:(Ⅰ)设PA中点为G,连结EG,DG. 因为PA∥BE,且PA=4,BE=2,
所以BE∥AG且BE=AG,
所以四边形BEGA为平行四边形.
所以EG∥AB,且EG=AB.
因为正方形ABCD,所以CD∥AB,CD=AB,
所以EG∥CD,且EG=CD.
所以四边形CDGE为平行四边形.
所以CE∥DG.
因为DG平面PAD,CE平面PAD,
所以CE∥平面PAD. 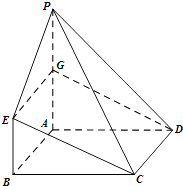
(Ⅱ)如图建立空间坐标系,则B(4,0,0),C(4,4,0),
E(4,0,2),P(0,0,4),D(0,4,0),
所以 ![]() =(4,4,﹣4),
=(4,4,﹣4), ![]() =(4,0,﹣2),
=(4,0,﹣2), ![]() =(0,4,﹣4).
=(0,4,﹣4).
设平面PCE的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
所以 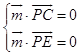 ,可得
,可得 ![]() .
.
令x=1,则 ![]() ,所以
,所以 ![]() =(1,1,2).
=(1,1,2).
设PD与平面PCE所成角为a,
则sinα=|cos< ![]() ,
, ![]() >|=|
>|=| 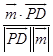 =|
=| ![]() |=
|= ![]() ..
..
所以PD与平面PCE所成角的正弦值是 ![]() .
. 
(Ⅲ)依题意,可设F(a,0,0),则 ![]() ,
, ![]() =(4,﹣4,2).
=(4,﹣4,2).
设平面DEF的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
则 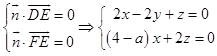 .
.
令x=2,则 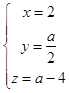 ,
,
所以 ![]() =(2,
=(2, ![]() ,a﹣4).
,a﹣4).
因为平面DEF⊥平面PCE,
所以 ![]() img src="http://thumb.zyjl.cn/questionBank/Upload/2017/07/19/20/d4b40ce9/SYS201707192041246227958281_DA/SYS201707192041246227958281_DA.015.png" width="13" height="23" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> =0,即2+
img src="http://thumb.zyjl.cn/questionBank/Upload/2017/07/19/20/d4b40ce9/SYS201707192041246227958281_DA/SYS201707192041246227958281_DA.015.png" width="13" height="23" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> =0,即2+ ![]() +2a﹣8=0,
+2a﹣8=0,
所以a= ![]() <4,点
<4,点 ![]() .
.
所以 ![]() .
. 
【解析】
【考点精析】本题主要考查了直线与平面平行的判定和空间角的异面直线所成的角的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 才能正确解答此题.
才能正确解答此题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,已知三棱锥P﹣ABC,PA⊥平面ABC,∠ACB=90°,∠BAC=60°,PA=AC,M为PB的中点. 
(Ⅰ)求证:PC⊥BC.
(Ⅱ)求二面角M﹣AC﹣B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着南宁三中集团化发展,南宁三中青三校区2018年被清华北大录取23人,广西领先,一本率连年攀升,南宁三中青山校区2014年至2018年一本率如下表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
时间代号 | 1 | 2 | 3 | 4 | 5 |
一本率 | 0.7152 | 0.7605 | 0.7760 | 0.8517 | 0.9015 |
(1)求![]() 关于
关于![]() 的回归方程
的回归方程![]() (精确到0.0001);
(精确到0.0001);
(2)用所求回归方程预测南宁三中青山校区2019年高考一本录取率.(精确到0.0001).
附:回归方程![]() 中
中
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】右图是一个几何体的平面展开图,其中ABCD为

正方形, E、F分别为PA、PD的中点,在此几何体中,
给出下面四个结论:
①直线BE与直线CF异面;②直线BE与直线AF异面;
③直线EF//平面PBC; ④平面BCE⊥平面PAD.
其中正确结论的个数是
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点A(0,4),且在两坐标轴上的截距之和为1.
(Ⅰ)求直线l的方程;
(Ⅱ)若直线l1与直线l平行,且l1与l间的距离为2,求直线l1的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣ ![]() ﹣2lnx,a∈R.
﹣2lnx,a∈R.
(1)讨论函数f(x)的单调性;
(2)若函数f(x)有两个极值点x1 , x2 , 且x1<x2 , 求a的取值范围;
(3)在(2)的条件下,证明:f(x2)<x2﹣1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】理科竞赛小组有9名女生、12名男生,从中随机抽取一个容量为7的样本进行分析.
(Ⅰ)如果按照性别比例分层抽样,可以得到多少个不同的样本?(写出算式即可)
(Ⅱ)如果随机抽取的7名同学的物理、化学成绩(单位:分)对应如表:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
物理成绩 | 65 | 70 | 75 | 81 | 85 | 87 | 93 |
化学成绩 | 72 | 68 | 80 | 85 | 90 | 86 | 91 |
规定85分以上(包括85份)为优秀,从这7名同学中再抽取3名同学,记这3名同学中物理和化学成绩均为优秀的人数为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF ![]() 2CE,G是线段BF上一点,AB=AF=BC.
2CE,G是线段BF上一点,AB=AF=BC. 
(Ⅰ)若EG∥平面ABC,求 ![]() 的值;
的值;
(Ⅱ)求二面角A﹣BF﹣E的大小的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂拟生产甲、乙两种实销产品.已知每件甲产品的利润为0.4万元,每件乙产品的利润为0.3万元,两种产品都需要在A,B两种设备上加工,且加工一件甲、乙产品在A,B设备上所需工时(单位:h)分别如表所示.
甲产品所需工时 | 乙产品所需工时 | |
A设备 | 2 | 3 |
B设备 | 4 | 1 |
若A设备每月的工时限额为400h,B设备每月的工时限额为300h,则该厂每月生产甲、乙两种产品可获得的最大利润为( )
A.40万元
B.45万元
C.50万元
D.55万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com