练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】有下列四个命题：

    （1）“若，则，互为倒数”的逆命题；

    （2）“面积相等的三角形全等”的否命题；

    （3）“若，则有实数解”的逆否命题；

    （4）“若，则”的逆否命题.

    其中真命题为（ ）

    A. （1）（2） B. （2）（3） C. （4） D. （1）（2）（3）

    【答案】D

    【解析】

    先根据逆命题、否命题、逆否命题定义得命题，再分别判断真假.

    （1）“若，则，互为倒数”的逆命题为“若，互为倒数，则”，为真命题；

    （2）“面积相等的三角形全等”的否命题为“面积不相等的三角形不全等”，为真命题；

    （3）“若，则有实数解”的逆否命题为“若无实数解，则”；因为，所以为真命题；

    （4）因为“若，则”为假命题，所以其逆否命题为假命题.

    综上选D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知中心在坐标原点，焦点在轴上的椭圆过点，且它的离心率

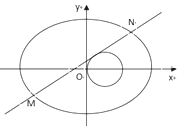
    （I）求椭圆的标准方程；

    （II）与圆相切的直线交椭圆于、两点，若椭圆上一点满足，求实数的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知椭圆（）的离心率为，以该椭圆上的点和椭圆的左、右焦点，为顶点的三角形的周长为，一等轴双曲线的顶点是该椭圆的焦点，设为该双曲线上异于顶点的任一点，直线和与椭圆的交点分别为、和、．

    （1）求椭圆和双曲线的标准方程；

    （2）设直线、的斜率分别为、，证明为定值；

    （3）是否存在常数，使得恒成立？若存在，求的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在多面体ABCDEF中，四边形ABCD为边长为4的正方形，M是BC的中点，EF∥平面ABCD，且EF=2，AE=DE=BF=CF= ．
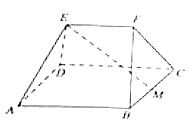
    （1）求证：ME⊥平面ADE；
    （2）求二面角B﹣AE﹣D的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着南宁三中集团化发展，南宁三中青三校区2018年被清华北大录取23人，广西领先，一本率连年攀升，南宁三中青山校区2014年至2018年一本率如下表：

    年份

    2014

    2015

    2016

    2017

    2018

    时间代号

    1

    2

    3

    4

    5

    一本率

    0.7152

    0.7605

    0.7760

    0.8517

    0.9015

    (1)求关于的回归方程 (精确到0.0001);

    (2)用所求回归方程预测南宁三中青山校区2019年高考一本录取率.(精确到0.0001).

    附：回归方程中

    参考数据：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工艺厂有铜丝5万米，铁丝9万米，准备用这两种材料编制成花篮和花盆出售，已知一只花篮需要用铜丝200米，铁丝300米；编制一只花盆需要100米，铁丝300米，设该厂用所有原来编制个花篮， 个花盆.

    （Ⅰ）列出满足的关系式，并画出相应的平面区域；

    （Ⅱ）若出售一个花篮可获利300元，出售一个花盘可获利200元，那么怎样安排花篮与花盆的编制个数，可使得所得利润最大，最大利润是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】右图是一个几何体的平面展开图，其中ABCD为

    正方形， E、F分别为PA、PD的中点，在此几何体中，

    给出下面四个结论：

    ①直线BE与直线CF异面；②直线BE与直线AF异面；

    ③直线EF//平面PBC； ④平面BCE⊥平面PAD.

    其中正确结论的个数是

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x﹣ ﹣2lnx，a∈R．
    （1）讨论函数f（x）的单调性；
    （2）若函数f（x）有两个极值点x1 ， x2 ， 且x1＜x2 ， 求a的取值范围；
    （3）在（2）的条件下，证明：f（x2）＜x2﹣1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，点O为数轴的原点，A，B，M为数轴上三点，C为线段OM上的动点．设x表示点C与原点的距离，y表示点C到点A的距离的4倍与点C到点B的距离的6倍之和．

    (1)将y表示为x的函数；

    (2)要使y的值不超过70，实数x应该在什么范围内取值？

    查看答案和解析>>

    同步练习册答案