
����Ŀ��ij���ճ���ͭ˿5���ף���˿9���ף����������ֲ��ϱ��Ƴɻ����ͻ�����ۣ���֪һֻ������Ҫ��ͭ˿200�ף���˿300�ף�����һֻ������Ҫ100�ף���˿300�ף���ó�������ԭ�����Ƹ�����![]() ��
�� ![]() ������.
������.
�����г�![]() ����Ĺ�ϵʽ����������Ӧ��ƽ������
����Ĺ�ϵʽ����������Ӧ��ƽ������
����������һ�������ɻ���300Ԫ������һ�����̿ɻ���200Ԫ����ô�������Ż����뻨��ı��Ƹ�������ʹ���������������������Ƕ��٣�
���𰸡���1������������2���ó�����200������,100����������������,�������Ϊ8��Ԫ.
�����������������(1)�г�x��y����Ĺ�ϵʽΪ ,��������ʽ������ʾ��ƽ������.
,��������ʽ������ʾ��ƽ������.
(2)��ó���������ΪzԪ,д��Ŀ�꺯��,����Ŀ�꺯���ļ�������,���Ŀ�꺯��z=300x+200y,���������.
���������
(1)����֪x��y����Ĺ�ϵʽΪ �ȼ���
�ȼ���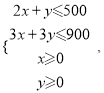
�ö�Ԫһ�β���ʽ������ʾ��ƽ��������ͼ�е���Ӱ����.

(2)��ó���������ΪzԪ,��Ŀ�꺯��Ϊz=300x+200y
��z=300x+200y����Ϊ![]() ,����б��Ϊ
,����б��Ϊ![]() ,��y���Ͻؾ�Ϊ
,��y���Ͻؾ�Ϊ![]() ����z�仯��һ��ƽ��ֱ��.
����z�仯��һ��ƽ��ֱ��.
����Ϊx��y����Լ������,������ͼ��֪,��ֱ��![]() �����������ϵĵ�Mʱ,�ؾ�
�����������ϵĵ�Mʱ,�ؾ�![]() ���,��z���.
���,��z���.
�ⷽ����![]() �õ�M������Ϊ(200,100)��ǡΪ����,��x=200,y=100.
�õ�M������Ϊ(200,100)��ǡΪ����,��x=200,y=100.
����, ![]() .
.
�𣺸ó�����200������,100����������������,�������Ϊ8��Ԫ.


 ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д� ����5��2���ϵ�д�
����5��2���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn���ΪSn �� ������2Sn+an=1�������ĵȲ�����{bn}����b1=1��b3=![]() ��4��
��4��
��1��������{an}��{bn}��ͨ�ʽ��
��2����cn��an �� bn�ĵȱ����������{![]() }��ǰn���Tn��
}��ǰn���Tn��
��3����c![]() ��
��![]() t2+2t��2��һ��������n���������ʵ��t��ȡֵ��Χ��
t2+2t��2��һ��������n���������ʵ��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���f(x)��x2��16x��q��3.
(1)������������[��1,1]�ϴ�����㣬��ʵ��q��ȡֵ��Χ��
(2)�Ƿ���ڳ���t(t��0)����x��[t,10]ʱ��f(x)��ֵ��Ϊ����D��������D�ij���Ϊ12��t(������[a��b]�ij���Ϊb��a)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֱ������ϵxOy�У�����C�IJ�������Ϊ ![]() Ϊ���������ڼ�����ϵ����ֱ������ϵxOyȡ��ͬ�ij��ȵ�λ������ԭ��OΪ���㣬��x��������Ϊ���ᣩ�У�ֱ��l�ķ���Ϊ��sin����+
Ϊ���������ڼ�����ϵ����ֱ������ϵxOyȡ��ͬ�ij��ȵ�λ������ԭ��OΪ���㣬��x��������Ϊ���ᣩ�У�ֱ��l�ķ���Ϊ��sin����+ ![]() ��=2
��=2 ![]() ��
��
��1��������C�ڼ�����ϵ�еķ��̣�
��2����ֱ��l������C�صõ��ҳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=2sin2x+cos��2x�� ![]() ����
����
������f��x������С�����ڣ�
������f��x���ڣ�0�� ![]() ���ϵĵ����������䣮
���ϵĵ����������䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��������Ϊ
��������Ϊ![]() �������ҽ���F����x�ᴹֱ��ֱ�߽���ԲC��P��Q���㣬��ԲC���Ҷ���ΪR��������
�������ҽ���F����x�ᴹֱ��ֱ�߽���ԲC��P��Q���㣬��ԲC���Ҷ���ΪR��������![]() .
.

(1)����ԲC�ķ��̣�
(2)��б��Ϊk(����![]() )��ֱ��l����F��������Բ���ڵ�A��B����AB���е�ΪM��ֱ��OM����Բ���ڵ�C��D�����ı���ACBD���
)��ֱ��l����F��������Բ���ڵ�A��B����AB���е�ΪM��ֱ��OM����Բ���ڵ�C��D�����ı���ACBD���![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() Ϊ������
Ϊ������![]() �Ľ��㣬����
�Ľ��㣬����![]() ��ֱ��
��ֱ��![]() ��
��![]() ����
����![]() ��
��![]() ���㣬
���㣬![]() ������
������![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() ������
������![]() ����
����![]() ��
��
��1�����![]() �Ĺ켣���̣�
�Ĺ켣���̣�
��2�����ı���![]() �������Сʱ����ֱ��
�������Сʱ����ֱ��![]() �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}����an+2= ![]() ����a1=1��a2=2��
����a1=1��a2=2��
��1����a3��a6+a9��a12+a15��ֵ��
��2��������{an}��ǰn���ΪSn �� ��Sn��2017ʱ����n����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ��˾�������98��Ԫ����һ���洬���ڲ��̣���һ������ַ���12��
Ԫ���ӵڶ��꿪ʼ����ά�����ڣ�ÿ��������þ�����һ������4��Ԫ���ô�ÿ�겶�̵�
������Ϊ50��Ԫ.
��1���ô����̼��꿪ʼӯ��(���������ȥ�ɱ������з���֮��Ϊ��ֵ)��
��2���ô�����������������������֣�
������ƽ��ӯ���ﵽ���ֵʱ����26��Ԫ�ļ۸�����;
����ӯ���ܶ�ﵽ���ֵʱ����8��Ԫ�ļ۸�����.����һ�ַ�����Ϊ���㣬��˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com