
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过其右焦点F且与x轴垂直的直线交椭圆C于P,Q两点,椭圆C的右顶点为R,且满足
,过其右焦点F且与x轴垂直的直线交椭圆C于P,Q两点,椭圆C的右顶点为R,且满足![]() .
.

(1)求椭圆C的方程;
(2)若斜率为k(其中![]() )的直线l过点F,且与椭圆交于点A,B,弦AB的中点为M,直线OM与椭圆交于点C,D,求四边形ACBD面积
)的直线l过点F,且与椭圆交于点A,B,弦AB的中点为M,直线OM与椭圆交于点C,D,求四边形ACBD面积![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】设椭圆![]() ,离心率
,离心率![]() ,短轴
,短轴![]() ,抛物线顶点在原点,以坐标轴为对称轴,焦点为
,抛物线顶点在原点,以坐标轴为对称轴,焦点为![]() ,
,
(1)求椭圆和抛物线的方程;
(2)设坐标原点为![]() ,
,![]() 为抛物线上第一象限内的点,
为抛物线上第一象限内的点,![]() 为椭圆是一点,且有
为椭圆是一点,且有![]() ,当线段
,当线段![]() 的中点在
的中点在![]() 轴上时,求直线
轴上时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线的方程为x2=2py(p>0),过点A(0,﹣1)作直线l与抛物线相交于P,Q两点,点B的坐标为(0,1),连接BP,BQ,设QB,BP与x轴分别相交于M,N两点.如果QB的斜率与PB的斜率的乘积为﹣3,则∠MBN的大小等于 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1,F2分别为双曲线![]() 的左、右焦点,A1,A2分别为这个双曲线的左、右顶点,P为双曲线右支上的任意一点.求证:以A1A2为直径的圆既与以PF2为直径的圆外切,又与以PF1为直径的圆内切.
的左、右焦点,A1,A2分别为这个双曲线的左、右顶点,P为双曲线右支上的任意一点.求证:以A1A2为直径的圆既与以PF2为直径的圆外切,又与以PF1为直径的圆内切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工艺厂有铜丝5万米,铁丝9万米,准备用这两种材料编制成花篮和花盆出售,已知一只花篮需要用铜丝200米,铁丝300米;编制一只花盆需要100米,铁丝300米,设该厂用所有原来编制个花篮![]() ,
, ![]() 个花盆.
个花盆.
(Ⅰ)列出![]() 满足的关系式,并画出相应的平面区域;
满足的关系式,并画出相应的平面区域;
(Ⅱ)若出售一个花篮可获利300元,出售一个花盘可获利200元,那么怎样安排花篮与花盆的编制个数,可使得所得利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,
中, ![]() 面
面![]() ,
, ![]() 是平行四边形,
是平行四边形, ![]() ,
, ![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且
上,且![]() ,平面
,平面![]() 与
与![]() 交于点
交于点![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成角的正切值为__________.
所成角的正切值为__________.
【答案】![]()
【解析】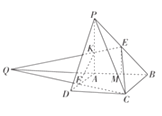
延长![]() 交
交![]() 的延长线与点Q,连接QE交PA于点K,设QA=x,
的延长线与点Q,连接QE交PA于点K,设QA=x,
由![]() ,得
,得![]() ,则
,则![]() ,所以
,所以![]() .
.
取![]() 的中点为M,连接EM,则
的中点为M,连接EM,则![]() ,
,
所以![]() ,则
,则![]() ,所以AK=
,所以AK=![]() .
.
由AD//BC,得异面直线![]() 与
与![]() 所成角即为
所成角即为![]() ,
,
则异面直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() .
.
【题型】填空题
【结束】
17
【题目】在极坐标系中,极点为![]() ,已知曲线
,已知曲线![]() :
: ![]() 与曲线
与曲线![]() :
: ![]() 交于不同的两点
交于不同的两点![]() ,
, ![]() .
.
(1)求![]() 的值;
的值;
(2)求过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,棱柱ABCD﹣A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,AB=1,AC= ![]() ,BC=BB1=2.
,BC=BB1=2. 
(Ⅰ)求证:AC⊥平面ABB1A1;
(Ⅱ)求二面角A﹣C1D﹣C的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD= ![]() ,AB=2,AD=1,若M、N分别是边AD、CD上的点,且满足
,AB=2,AD=1,若M、N分别是边AD、CD上的点,且满足 ![]() =λ,其中λ∈[0,1],则
=λ,其中λ∈[0,1],则 ![]() 的取值范围是( )
的取值范围是( ) 
A.[﹣3,﹣1]
B.[﹣3,1]
C.[﹣1,1]
D.[1,3]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com