
思路分析:判定两个变量是否构成函数,关键看两个变量之间的对应关系是否满足函数定义.该题中的每一个腰长都能对应唯一的周长值,因此周长y是腰长x的函数.若要用腰长表示周长的关系式,应知等腰梯形各边长,下底长已知为2R,两腰长为2x,因此只需用已知量(半径R)和腰长x把上底表示出来,即可写出周长与腰长的函数关系式.
解:由题意可知,每一个腰长x都能对应唯一的周长值y,因此周长y是腰长x的函数.
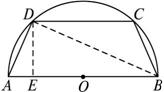
如下图,

AB=2R,C、D在⊙O的半圆周上,设腰长AD=BC=x,作DE⊥AE,垂足为E,连结BD,那么∠ADB是直角,由此Rt△ADE∽Rt△ABD.
∴AD2=AE·AB,即AE=![]() .
.
∴CD=AB-2AE=2R-![]() .
.
∴周长y满足关系式
y=2R+2x+(2R-![]() )=-
)=-![]() +2x+4R,
+2x+4R,
即周长y和腰长x间的函数关系式y=-![]() +2x+4R.
+2x+4R.
∵ABCD是圆内接梯形,∴AD>0,AE>0,CD>0,即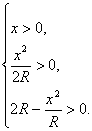 解不等式组,得函数y的定义域为{x|0<x<
解不等式组,得函数y的定义域为{x|0<x<![]() R}.
R}.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
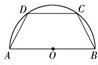 如右图所示,有一块半径为R的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,且上底CD的端点在圆周上,写出梯形周长y关于腰长x的函数关系式,并求出它的定义域.
如右图所示,有一块半径为R的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,且上底CD的端点在圆周上,写出梯形周长y关于腰长x的函数关系式,并求出它的定义域.查看答案和解析>>
科目:高中数学 来源: 题型:
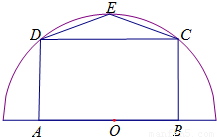
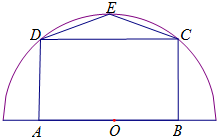 如图,有一块半径为R的半圆形空地,开发商计划征地建一个矩形游泳池ABCD和其附属设施,附属设施占地形状是等腰△CDE,其中O为圆心,A,B在圆的直径上,C,D,E在圆周上.
如图,有一块半径为R的半圆形空地,开发商计划征地建一个矩形游泳池ABCD和其附属设施,附属设施占地形状是等腰△CDE,其中O为圆心,A,B在圆的直径上,C,D,E在圆周上.查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,有一块半径为R的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O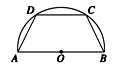
的直径,且上底CD的端点在圆周上,写出梯形周长y关于腰长x的函数关系式,并求出它的定义域.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省镇江市高二(上)期末数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com