解:(1)∵
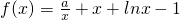
∴f′(x)=
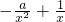
=
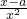
,令f′(x)=0得,x=a,
①若0<a<e,当x∈(0,a)时,f′(x)<0,函数f(x)在区间(0,a)上单调递减,当x∈(a,e)时,f′(x)>0,函数f(x)在区间(a,e)上单调递增,
所以当x=a时,函数f(x)在区间(0,e]上取得最小值lna.
②若a≥e,则f′(x)≤0,函数f(x)在区间(0,e]上单调递减,所以当x=e时,函数f(x)在区间(0,e]上取得最小值

.;
综上所述,当0<a<e时,函数f(x)在区间(0,e]上取得最小值lna,当a≥e时,函数f(x)在区间(0,e]上取得最小值

.;
(2)不存在.证明如下

,x∈(0,e],
∴g′(x)=

•e
x+(lnx-1)e
x+1=(

+lnx-1)e
x+1
由(1)知,当a=1时,

,此时f(x)在区间(0,e]上取得最小值ln1=0,即
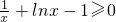
,而e
x>0,所以g′(x)≥1>0,
又曲线y=g(x)在点x=x
0处的切线与y轴垂直,等价于g′(x
0)=0有实数根,而g′(x)>0,所以方程g′(x
0)=0无实数根,
故不存在实数x
0∈(0,e],使曲线y=g(x)在点x=x
0处的切线与y轴垂直.
分析:(1)得出f′(x)=
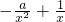
=
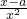
,利用函数单调性与导数的关系寻求f(x)在区间(0,e]上单调性,得出最小值.
(2)曲线y=g(x)在点x=x
0处的切线与y轴垂直,等价于g′(x
0)=0有实数根.g′(x)=

•e
x+(lnx-1)e
x+1=(

+lnx-1)e
x+1其中括号内部分正好为当a=1时,

,利用(1)的结论,得出g′(x)>0,所以方程g′(x
0)=0无实数根,故不存在.
点评:本题考查函数单调性与导数的关系,函数最值求解,导数的几何意义,考查分类讨论、转化、整体代换、计算能力.是好题.

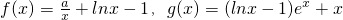 (其中e为自然对数的底).
(其中e为自然对数的底).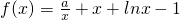 ∴f′(x)=
∴f′(x)=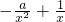 =
=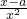 ,令f′(x)=0得,x=a,
,令f′(x)=0得,x=a, .;
.; .;
.; ,x∈(0,e],
,x∈(0,e], •ex+(lnx-1)ex+1=(
•ex+(lnx-1)ex+1=( +lnx-1)ex+1
+lnx-1)ex+1 ,此时f(x)在区间(0,e]上取得最小值ln1=0,即
,此时f(x)在区间(0,e]上取得最小值ln1=0,即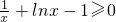 ,而ex>0,所以g′(x)≥1>0,
,而ex>0,所以g′(x)≥1>0,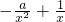 =
=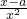 ,利用函数单调性与导数的关系寻求f(x)在区间(0,e]上单调性,得出最小值.
,利用函数单调性与导数的关系寻求f(x)在区间(0,e]上单调性,得出最小值. •ex+(lnx-1)ex+1=(
•ex+(lnx-1)ex+1=( +lnx-1)ex+1其中括号内部分正好为当a=1时,
+lnx-1)ex+1其中括号内部分正好为当a=1时, ,利用(1)的结论,得出g′(x)>0,所以方程g′(x0)=0无实数根,故不存在.
,利用(1)的结论,得出g′(x)>0,所以方程g′(x0)=0无实数根,故不存在.

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案