
已知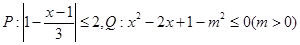 ,又知非
,又知非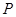 是非
是非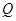 的必要非充分条件,则
的必要非充分条件,则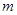 的取值范围是 .
的取值范围是 .
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
在整数集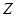 中,被5除所得余数为
中,被5除所得余数为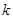 的所有整数组成一个“类”,记为
的所有整数组成一个“类”,记为 ,即
,即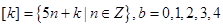 ,则下列结论正确的为 (写出所有正确的编号).
,则下列结论正确的为 (写出所有正确的编号).
①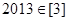 ;
;
②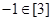 ;
;
③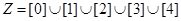 ;
;
④“整数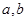 属于同一类”的充要条件是“
属于同一类”的充要条件是“ ”;
”;
⑤命题“整数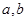 满足
满足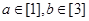 ,则
,则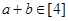 ”的原命题与逆命题都为真命题.
”的原命题与逆命题都为真命题.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
给出下列四个命题:
①若f(x+2)=f(2-x),则f(x)的图象关于x=2对称;
②若f(x+2)=f(2-x),则f(x)的图象关于y轴对称;
③函数y=f(2+x)与y=f(2-x)的图象关于x=2对称;
④函数y=f(2+x)与y=f(2—x)的图象关于y轴对称。正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知下列几个命题: ①已知F1、F2为两定点, =4,动点M满足
=4,动点M满足 ,则动点M的轨迹是椭圆。 ②一个焦点为
,则动点M的轨迹是椭圆。 ②一个焦点为 且与双曲线
且与双曲线 有相同的渐近线的双曲线标准方程是
有相同的渐近线的双曲线标准方程是 ③“若
③“若 =b,则a2=ab”的否命题。④若一个动圆的圆心在抛物线
=b,则a2=ab”的否命题。④若一个动圆的圆心在抛物线 上,且动圆恒与直线
上,且动圆恒与直线 相切,则动圆必过定点
相切,则动圆必过定点 。
。
其中真命题有____________
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
给出下列四个结论:
① 若角的集合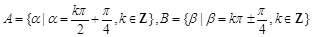 ,则
,则 ;
;
② 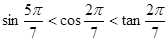
③  是函数
是函数 的单调递减区间
的单调递减区间
④ 函数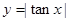 的周期和对称轴方程分别为
的周期和对称轴方程分别为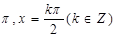
其中正确结论的序号是 .(请写出所有正确结论的序号)。
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
给出下列四个判断,(1)若 ;(2)对判断“
;(2)对判断“ 都大于零”的反设是“
都大于零”的反设是“ 不都大于零”;(3)“
不都大于零”;(3)“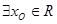 ,使得
,使得 ”的否定是“对
”的否定是“对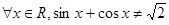 ”;(4)某产品销售量
”;(4)某产品销售量 (件)与销售价格
(件)与销售价格 (元/件)负相关,则其回归方程
(元/件)负相关,则其回归方程 ,以上判断正确的是_________。
,以上判断正确的是_________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com