分析:(1)先判断出结论,线与面平行,再作辅助线证明线面平行,由线面平行的判定定理知,须先证线线平行,由图形知延长B1E交BC的延长线于M,证明CM∥AD即可
(2)证明面面垂直要用面面垂直的判定理,由题意知可证明DM⊥平面BDB1及DM?平面B1DE证明平面B1DE⊥平面B1BD;
(3)求二面角平面角,要先作角,证角,再求角,由图形知作BH⊥B1D于H,由(2)知BH⊥平面B1DE,作OH⊥B1E于O,连接BO,则BO⊥B1E,由此得∠BOH为二面角B-B1E-D的平面角.
解答:解:
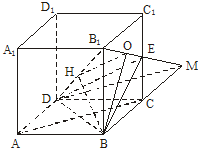
(1)线与面是平行的关系,证明如下:
延长B
1E交BC的延长线于M,
∵E为CC
1的中点,
∴Rt△ECM≌Rt△EC
1B
1.
∴CM=B
1C
1=AD.又CM∥AD,
∴ACMD为平行四边形.
∴AC∥DM.
又AC平面B
1DE,DM?平面B
1DE,
∴AC∥平面B
1DE.(5分)
(2)证明:∵BB
1⊥平面ABCD,
∴BB
1⊥AC.
又ABCD为正方形,
∴BD⊥AC.
∴AC⊥平面BDB
1.
∵DM∥AC,
∴DM⊥平面BDB
1.
又DM?平面B
1DE,
∴平面B
1DE⊥平面B
1BD.(10分)
(3)解:作BH⊥B
1D于H,由(2)知BH⊥平面B
1DE,作OH⊥B
1E于O,连接BO,则BO⊥B
1E,
∴∠BOH为二面角B-B
1E-D的平面角.
在Rt△B
1BD中,BH=
=
,连接BE,则BO是等腰△BB
1E的腰B
1E上的高,
∴BO=
=
.
在Rt△BHO中,sin∠BOH=
=
,
∴二面角B
1-BE-D的大小为arcsin
.(14分)
点评:本题主要考查了直线与平面平行的判定,面面垂直的证明以及二面角的度量等基础知识,考查空间想象能力,运算能力和推理论证能力,属于难度较高的题,本题解题的关键是找出二面角的平面角,放在一个可解的三角形中解出结果.

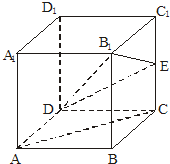 在正方体ABCD-A1B1C1D1中,E是棱CC1的中点.
在正方体ABCD-A1B1C1D1中,E是棱CC1的中点. (1)线与面是平行的关系,证明如下:
(1)线与面是平行的关系,证明如下:

 16、在正方体ABCD-A′B′C′D′中,过对角线BD′的一个平面交AA′于E,交CC′于F,则
16、在正方体ABCD-A′B′C′D′中,过对角线BD′的一个平面交AA′于E,交CC′于F,则 如图,在正方体ABCD-A′B′C′D′中,E,F分别是AB′,BC′的中点.
如图,在正方体ABCD-A′B′C′D′中,E,F分别是AB′,BC′的中点.