Question

袋中装着标有数字1、2、3、4、5的小球各2个，从袋中任取3个小球，每个小球被取出的可能性都相等，用ξ表示取出的3个小球上的最大数字，求：
（1）取出的3个小球上的数字互不相同的概率；
（2）随机变量ξ的概率分布列和数学期望．

Answer 1

分析：（1）根据题意，一次取出的3个小球上的数字互不相同的事件记为A，一次取出的3个小球上有两个数字相同的事件记为B，易得事件A和事件B是互斥事件，易得事件B的概率，由互斥事件的意义，可得答案，
（2）由题意ξ有可能的取值为：2，3，4，5，分别计算其取不同数值时的概率，列出分步列，进而计算可得答案．

解答：解：（1）一次取出的3个小球上的数字互不相同的事件记为A，一次取出的3个小球上有两个数字相同的事件记为B，则事件A和事件B是互斥事件，因为P(B)=

C 1 5 • C 2 2 • C 1 8

C 3 10

=

1

3

所以P(A)=1-P(B)=1-

1

3

=

2

3

．（4分）
（2）由题意ξ有可能的取值为：2，3，4，5．（5分）
P(ξ=2)=

C 2 2 • C 1 2 + C 1 2 • C 2 2

C 3 10

=

1

30

；（8分）
P(ξ=3)=

C 2 4 • C 1 2 + C 1 4 • C 2 2

C 3 10

=

2

15

；（9分
）P(ξ=4)=

C 2 6 • C 1 2 + C 1 6 • C 2 2

C 3 10

=

3

10

；（10分）
P(ξ=5)=

C 2 8 • C 1 2 + C 1 8 • C 2 2

C 3 10

=

8

15

；（11分）
所以随机变量ε的概率分布为
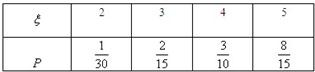
（12分）
因此ξ的数学期望为：Eξ=2×

1

30

+3×

2

15

+4×

3

10

+5×

8

15

=

13

3

（14分）

点评：本题考查概率的计算以及随机变量的分布列的运用，注意其公式的正确运用即可．