
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $2\sqrt{3}$ | C. | $\frac{{2\sqrt{6}}}{3}$ | D. | $2\sqrt{6}$ |
分析 取AC中点E,连结BE、DE,则∠BED=60°,由此求出BD=$\sqrt{6}$,从而能求出四面体D-ABC的体积.
解答 解: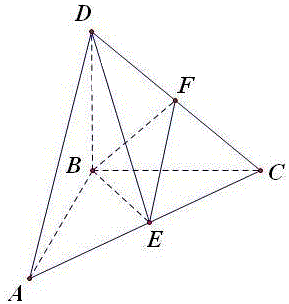 如图,∵面体D-ABC中,BA,BC,BD两两垂直,且AB=BC=2,
如图,∵面体D-ABC中,BA,BC,BD两两垂直,且AB=BC=2,
∴BD⊥平面ABC,
取AC中点E,连结BE、DE,则BE⊥AC,∴DE⊥AC,
∴∠BED是二面角D-AC-B的平面角,
∵二面角D-AC-B的大小为60°,∴∠BED=60°,
∴∠BDE=30°,
∵BE=$\frac{1}{2}\sqrt{4+4}$=$\sqrt{2}$,(2BE)2=BE2+BD2,
解得BD=$\sqrt{6}$,
∴四面体D-ABC的体积:
V=$\frac{1}{3}×{S}_{△ABC}×DB$=$\frac{1}{3}×\frac{1}{2}×2×2×\sqrt{6}$=$\frac{2\sqrt{6}}{3}$.
故选:C.
点评 本题考查四面体的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若p∨q为真命题,则p∧q为真命题 | |
| B. | “a>0,b>0”是“$\frac{b}{a}+\frac{a}{b}≥2$”的充分必要条件 | |
| C. | 命题“若x2-3x+2=0,则x=1或x=2”的逆否命题为“若x≠1或x≠2,则x2-3x+2≠0” | |
| D. | 命题p:?x0>0,使得$x_0^2+{x_0}-1<0$,则¬p:?x>0,使得x2+x-1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
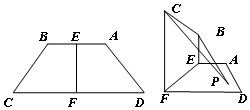 如图,在等腰梯形ABCD中,CD=2AB=2EF=2a,E,F分别是底边AB,CD的中点,把四边形BEFC沿直线EF折起,使得平面BEFC⊥平面ADFE.若动点P∈平面ADFE,设PB,PC与平面ADFE所成的角分别为θ1,θ2(θ1,θ2均不为0).若θ1=θ2,则动点P的轨迹围成的图形的面积为( )
如图,在等腰梯形ABCD中,CD=2AB=2EF=2a,E,F分别是底边AB,CD的中点,把四边形BEFC沿直线EF折起,使得平面BEFC⊥平面ADFE.若动点P∈平面ADFE,设PB,PC与平面ADFE所成的角分别为θ1,θ2(θ1,θ2均不为0).若θ1=θ2,则动点P的轨迹围成的图形的面积为( )| A. | $\frac{1}{4}{a^2}$ | B. | $\frac{4}{9}{a^2}$ | C. | $\frac{1}{4}π{a^2}$ | D. | $\frac{4}{9}π{a^2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com