练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    当x＝时，函数y＝f(x)＝Asin(x＋φ)(A＞0)取得最小值，则函数y＝f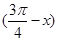是（    ）

    A．奇函数且当x＝时取得最大值     B．偶函数且图象关于点(π，0)对称

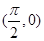    C．奇函数且当x＝时取得最小值     D．偶函数且图象关于点对称

     

    【答案】

    C

    【解析】

    试题分析：因为，所以所以y＝f是奇函数且当x＝时取得最小值.

    考点：本小题主要考查三角函数最值、奇偶性及诱导公式的应用，考查了学生分析问题、解决问题的能力.

    点评：三角函数的图象和性质是高考考查的重点，要牢记图象和性质并灵活应用.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：学习周报　数学　人教课标高一版(A必修1)　2009－2010学年　第13期　总169期 人教课标高一版 题型：022

    当x∈R时，函数y＝f(x)满足f(2002＋x)＋f(2004＋x)＝f(2003＋x)，且f(1)＝lg，f(2)＝lg15，则f(2010)＝________．

    查看答案和解析>>

    科目：高中数学 来源：重庆市西南师大附中2010届高三第四次月考、理科数学试卷 题型：013

    已知当x∈R时，函数y＝f(x)满足f(2.5＋x)＝f(1.5＋x)＋，且f(1)＝，则f(2010)的值为

    [　　]
    A．

    B．

    C．

    671

    D．

    268

    查看答案和解析>>

    科目：高中数学 来源：重庆市西南师大附中2010届高三第四次月考、文科数学试卷 题型：013

    已知当x∈R时，函数y＝f(x)满足f(2.5＋x)＝f(1.5＋x)＋，且f(1)＝，则f(2010)的值为

    [　　]
    A．

    B．

    C．

    671

    D．

    268

    查看答案和解析>>

    科目：高中数学 来源：新课标高三数学函数专项训练（河北） 题型：解答题

    已知函数f(x)＝()x，

    函数y＝f－1(x)是函数y＝f(x)的反函数．

    (1)若函数y＝f－1(mx2＋mx＋1)的定义域为R，求实数m的取值范围；

    (2)当x∈[－1,1]时，求函数y＝[f(x)]2－2af(x)＋3的最小值g(a)；

    (3)是否存在实数m＞n＞3，使得g(x)的定义域为[n，m]，值域为[n2，m2]？若存在，求出m、n的值；若不存在，请说明理由

     

    查看答案和解析>>

    同步练习册答案