
【题目】已知函数![]() ,
,
(Ⅰ)若![]() ,且
,且![]() 是函数的一个极值,求函数
是函数的一个极值,求函数![]() 的最小值;
的最小值;
(Ⅱ)若![]() ,求证:
,求证:![]() ,
,![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】分析:(I)由函数的解析式可得![]() .结合
.结合![]() ,可得
,可得![]() , 利用导函数研究函数的单调性可得
, 利用导函数研究函数的单调性可得![]() 在
在![]() 上单调递减,
上单调递减,![]() 在
在![]() 上单调递增,函数
上单调递增,函数![]() 的最小值为
的最小值为![]() .
.
(II )若![]() ,则
,则![]() ,
,![]() ,
,
由![]() 在
在![]() 上单调递增,分类讨论:
上单调递增,分类讨论:
①当![]() 在
在![]() 上单调递增时,
上单调递增时,![]() ;
;
②当![]() 在
在![]() 上单调递减时,
上单调递减时,![]() ;
;
③当![]() 在
在![]() 上先减后增时,
上先减后增时,![]() ,
,![]() ,
,![]()
![]() ,
,
综上①②③得:![]() ,
,![]() .
.
详解:(I)![]() ,定义域为
,定义域为![]() ,
,
![]() .
.
由题意知![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以![]() ,
,![]() ,
,
又![]() 、
、![]() 、
、![]() (
(![]() )在
)在![]() 上单调递增,
上单调递增,
可知![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
得![]() 在
在![]() 上单调递减,
上单调递减,![]() 在
在![]() 上单调递增,
上单调递增,
所以函数![]() 的最小值为
的最小值为![]() .
.
(II )若![]() ,得
,得![]() ,
,![]()
由![]() 在
在![]() 上单调递增,可知
上单调递增,可知![]() 在
在![]() 上的单调性有如下三种情形:
上的单调性有如下三种情形:
①当![]() 在
在![]() 上单调递增时,
上单调递增时,
可知![]() ,即
,即![]() ,即
,即![]() ,解得
,解得![]() ,
,
![]() ,令
,令![]() ,则
,则![]() ,
,
所以![]() 单调递增,
单调递增,![]() ,所以
,所以![]() ;
;
②当![]() 在
在![]() 上单调递减时,
上单调递减时,
可知![]() ,即
,即![]() ,即
,即![]() ,解得
,解得![]() ,
,
得![]() ,所以
,所以![]() ;
;
[或:令![]() ,则
,则![]() ,
,
所以![]() 单调递减,
单调递减,![]() ,所以
,所以![]() ;]
;]
③当![]() 在
在![]() 上先减后增时,得
上先减后增时,得![]() 在
在![]() 上先负后正,
上先负后正,
所以![]() ,
,![]() ,即
,即![]() ,取对数得
,取对数得![]() ,
,
可知![]()
![]()
![]() ,
,
所以![]() ;
;
综上①②③得:![]() ,
,![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 经过点
经过点![]() ,离心率为
,离心率为![]() .
.
(1)求![]() 的方程;
的方程;
(2)过![]() 的左焦点
的左焦点![]() 且斜率不为
且斜率不为![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,若
,若![]() 为等腰直角三角形,求
为等腰直角三角形,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只药用昆虫的产卵数![]() 与一定范围内的温度
与一定范围内的温度![]() 有关,现收集了该种药用昆虫的
有关,现收集了该种药用昆虫的![]() 组观测数据如下表:
组观测数据如下表:
温度 |
|
|
|
|
|
|
产卵数 |
|
|
|
|
|
|
经计算得: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,线性回归模型的残差平方和
,线性回归模型的残差平方和![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() 分别为观测数据中的温差和产卵数,
分别为观测数据中的温差和产卵数, ![]() .
.
(1)若用线性回归方程,求![]() 关于
关于![]() 的回归方程
的回归方程![]() (精确到
(精确到![]() );
);
(2)若用非线性回归模型求得![]() 关于
关于![]() 回归方程为
回归方程为![]() ,且相关指数
,且相关指数![]() .
.
(i)试与(1)中的回归模型相比,用![]() 说明哪种模型的拟合效果更好.
说明哪种模型的拟合效果更好.
(ii)用拟合效果好的模型预测温度为![]() 时该种药用昆虫的产卵数(结果取整数).
时该种药用昆虫的产卵数(结果取整数).
附:一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为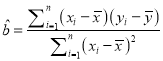 ,
, ![]() ;相关指数
;相关指数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解中学生对交通安全知识的掌握情况,从农村中学和城镇中学各选取100名同学进行交通安全知识竞赛.下图1和图2分别是对农村中学和城镇中学参加竞赛的学生成绩按![]() ,
,![]() ,
,![]() ,
,![]() 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.
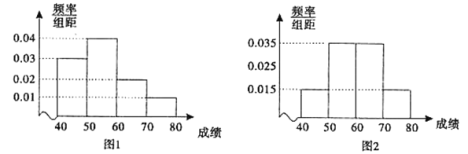
(Ⅰ)分别估算参加这次知识竞赛的农村中学和城镇中学的平均成绩;
(Ⅱ)完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“农村中学和城镇中学的学生对交通安全知识的掌握情况有显著差异”?
的把握认为“农村中学和城镇中学的学生对交通安全知识的掌握情况有显著差异”?
成绩小于60分人数 | 成绩不小于60分人数 | 合计 | |
农村中学 | |||
城镇中学 | |||
合计 |
附:![]()
临界值表:
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,离心率为
,离心率为![]() .
.
(![]() )求椭圆
)求椭圆![]() 的方程.
的方程.
(![]() )直线
)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 的右顶点.直线
的右顶点.直线![]() 与直线
与直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
,![]() 两点,试问在
两点,试问在![]() 轴上是否存在一个定点
轴上是否存在一个定点![]() 使得
使得![]() ?若是,求出定点
?若是,求出定点![]() 坐标;若不是,说明理由.
坐标;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视厂家准备在五一举行促销活动,现在根据近七年的广告费与销售量的数据确定此次广告费支出.广告费支出x(万元)和销售量y(万台)的数据如下:

(1)若用线性回归模型拟合y与x的关系,求出y关于x的线性回归方程(其中![]() ;参考方程:回归直线
;参考方程:回归直线 ,
,![]() )
)
(2)若用模型![]() 拟合y与x的关系,可得回归方程
拟合y与x的关系,可得回归方程![]() ,经计算线性回归模型和该模型的
,经计算线性回归模型和该模型的![]() 分别约为0.75和0.88,请用
分别约为0.75和0.88,请用![]() 说明选择哪个回归模型更好;
说明选择哪个回归模型更好;
(3)已知利润z与x,y的关系为z=200y﹣x.根据(2)的结果回答:当广告费x=20时,销售量及利润的预报值是多少?(精确到0.01)参考数据:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com