
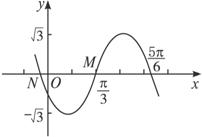
剖析:本题主要考查正弦函数的图象与性质.
首先确定A,若以N为五点法作图中的第一个零点,由于此时曲线是先下降后上升(类似于y=-sinx的图象),所以A<0;若以M点为第一个零点,由于此时曲线是先上升后下降(类似于y=sinx的图象),所以A>0.而ω=![]() ,φ可由相位来确定.
,φ可由相位来确定.
解法一:以N为第一个零点,
则A=-![]() ,T=2(
,T=2(![]() -
-![]() )=π.
)=π.
∴ω=2.
此时解析式为y=-![]() sin(2x+φ).
sin(2x+φ).
∵点N(-![]() ,0),
,0),
∴-![]() ×2+φ=0
×2+φ=0![]() φ=
φ=![]() .
.
所求解析式为y=-![]() sin(2x+
sin(2x+![]() ).①
).①
解法二:以点M(![]() ,0)为第一个零点,
,0)为第一个零点,
则A=![]() ,ω=
,ω=![]() =2.
=2.
解析式为y=![]() sin(2x+φ).
sin(2x+φ).
将点M坐标代入得2×![]() +φ=0
+φ=0![]() φ=-
φ=-![]() .
.
∴所求解析式为y=![]() sin(2x-
sin(2x-![]() ).②
).②


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
函数y=Asin(ωx+φ)的图象的一部分如下图所示,那么其一个解析式为( )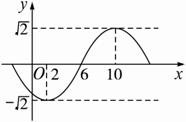
A.y=![]() sin(
sin(![]() x-
x-![]() ) B.y=
) B.y=![]() sin(
sin(![]() -
-![]() )
)
C.y=![]() sin(
sin(![]() -
-![]() ) D.y=
) D.y=![]() sin(
sin(![]()
![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com