练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    圆C：x2+y2-2x-4y+4=0的圆心到直线l：3x+4y+4=0的距离为（　　）
    A、3
    		5
    B、2
    C、3
    D、
    		5
    考点：点到直线的距离公式
    专题：直线与圆
    分析：由圆C：x2+y2-2x-4y+4=0配方得到（x-1）2+（y-2）2=1，即可得到圆心C（1，2）．再利用圆心到直线的距离公式即可得出．
    解答： 解：由圆C：x2+y2-2x-4y+4=0配方得到（x-1）2+（y-2）2=1，得到圆心C（1，2）．
    ∴圆心C（1，2）到直线l：3x+4y+4=0的距离d=
    |3×1+4×2+4|
    		32+42
    =3．
    故选：C．
    点评：本题考查了圆的标准方程、配方法、点到直线的距离公式，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    为了判断高中三年级学生选修文科是否与性别有关，现随机抽取50名学生，得到如2×2列联表：可得到的正确结论是（　　）（Χ2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    ），
    理科 文科 合计
    男 13 10 23
    女 7 20 27
    合计 20 30 50
    A、在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”
    B、在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”
    C、有95%以上的把握认为“爱好该项运动与性别有关”
    D、有99%以上的把握认为“爱好该项运动与性别有关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知直线l1：ax+2y-1=0与直线l2：ax-2y-3=0，“a=2”是“l1的方向向量是l2的法向量”的（　　）
    A、充分非必要条件
    B、必要非充分条件
    C、充要条件
    D、既非充分又非必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    双曲线x2-
    y2
    9
    =1    的实轴长为（　　）
    A、4B、3C、2D、1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，函数y=f（x）的图象在点P处的切线方程是y=-x+8，则f′（5）=（　　）
    A、
    1
    2
    B、1
    C、-1
    D、0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    曲线f（x）=x2+3x在x=-1处的切线方程为（　　）
    A、x-y+1=0
    B、x-y-1=0
    C、2x+y+4=0
    D、2x+y-4=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    椭圆有一个焦点固定，并通过两个已知点，且该焦点到这两个定点不等距．则该椭圆另一个焦点的轨迹类型是（　　）
    A、椭圆型B、双曲线型
    C、抛物线型D、非圆锥曲线型

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
    π
    2
    ）的图象的一部分如图所示：
    （1）求函数f（x）的解析式，并写出它的单调减区间；
    （2）当x∈[-6，-
    2
    3
    ]时，求函数y=f（x+2）的值域；
    （3）记S=f（0）+f（1）+…+f（2014），求S的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

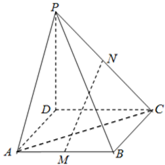    如图，P是正方形ABCD所在平面外一点，且PD⊥AD，PD⊥DC，PD=3，AD=2，若M、N分别是AB、PC的中点．
    （1）求证：MN⊥DC；
    （2）求点M到平面PAC的距离．

    查看答案和解析>>

    同步练习册答案