已知函数y=f(x)=loga(1-ax)(a>0且a≠1).
(1)求f(x)的定义域、值域;
(2)证明f(x)在定义域上是减函数.
解:(1)由1-a
x>0,得a
x<1.(1分)
当a>1时,x<0;(2分)
当0<a<1时,x>0.(3分)
所以f(x)的定义域是当0<a<1时,x∈(0,+∞);当a>1时,x∈(-∞,0).(4分)
又当a>1时,x<0,?1>1-a
x>0,?log
a(1-a
x)<0,即函数的值域为(-∞,0).
当时,x>0,?1>1-a
x>0,?log
a(1-a
x)>0,即函数的值域为(0,+∞).
所以f(x)的值域是,当0<a<1时,y∈(0,+∞);当a>1时,y∈(-∞,0).
(2)当0<a<1时,任取x
1、x
2∈(0,+∞),且x
1<x
2,(5分)
则

,所以
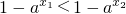
.(6分)
因为0<a<1,所以
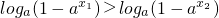
,即f(x
1)>f(x
2).(8分)
故当0<a<1时,f(x)在(0,+∞)上是减函数.(9分)
同理,当a>1时,任取x
1、x
2∈(-∞,0),且x
1<x
2,(10分)
可得当a>1时,f(x)在(-∞,0)上也是减函数.(14分).
分析:(1)由1-a
x>0,得a
x<1 下面分类讨论:当a>1时,x<0;当0<a<1时,x>0即可求得f(x)的定义域及值域;
(2)先对a值进行分类讨论:当a>1时,当0<a<1时,再任取x
1、x
2属于集合范围之内,结合函数的单调性的定义讨论函数f(x)的单调性.
点评:本小题主要考查函数单调性的应用、对数函数的定义域值域、不等式的解法等基础知识,考查运算求解能力与转化思想.属于基础题.

 ,所以
,所以 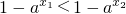 .(6分)
.(6分)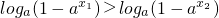 ,即f(x1)>f(x2).(8分)
,即f(x1)>f(x2).(8分)

 阅读快车系列答案
阅读快车系列答案 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为