
(1)用反证法证明:在一个三角形中,至少有一个内角大于或等于 ;
;
(2)已知 ,试用分析法证明:
,试用分析法证明: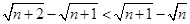 .
.
(1)证明详见解析;(2)证明详见解析.
解析试题分析:(1)根据应用反证法证明命题的一般步骤,先假设原命题的结论不成立,由此找出矛盾(本题中的矛盾指向:三角形的内角和定理),从而肯定结论进行证明即可;(2)根据分析法的思路是执果索因,要证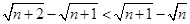 ,只需证
,只需证 ,进而结合不等式的性质:不等式的可乘方性,进行逐渐整理即可得到最后只须证
,进而结合不等式的性质:不等式的可乘方性,进行逐渐整理即可得到最后只须证 ,显然
,显然 成立,从而命题得证.
成立,从而命题得证.
试题解析:(1)证明:假设在一个三角形中,没有一个内角大于或等于 ,即均小于
,即均小于
则三内角和小于 ,与三角形中三内角和等于
,与三角形中三内角和等于 矛盾,故假设不成立,原命题成立;
矛盾,故假设不成立,原命题成立;
(2)证明:要证上式成立,需证
需证
需证
需证
需证
只需证
因为 显然成立,所以原命题成立.
显然成立,所以原命题成立.
考点:1.反证法;2.分析法.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:高中数学 来源: 题型:解答题
若函数 满足:集合
满足:集合 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数 是等比源函数.
是等比源函数.
(1)判断下列函数:① ;②
;② 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明)
(2)证明:对任意的正奇数 ,函数
,函数 不是等比源函数;
不是等比源函数;
(3)证明:任意的 ,函数
,函数 都是等比源函数.
都是等比源函数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
观察以下等式:
sin230°+cos260°+sin 30°·cos 60°= ,
,
sin240°+cos270°+sin 40°·cos 70°= ,
,
sin215°+cos245°+sin 15°·cos 45°= .
.
…
写出反映一般规律的等式,并给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com