
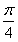 ,OA⊥底面ABCD,OA=2, M为OA的中点,N为BC的中点。
,OA⊥底面ABCD,OA=2, M为OA的中点,N为BC的中点。 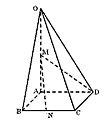
(1)证明:取OB中点E,连结ME,NE,
∵ME∥AB,AB∥CD,
∴ME∥CD,
又∵NE∥OC,
∴平面MNE∥平面OCD,
∴MN∥平面OCD。
(2)解:∵CD∥AB,
∴∠MDC(或其补角)为异面直线AB与MD所成的角,
作AP⊥CD于P,连结MP,
∵OA⊥平面ABCD,
∴CD⊥MP,
∵∠ADP=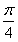 ,
,
∴DP=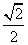 ,
,
∵MD=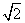 ,
,
∴cos∠MDP=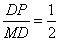 ,∠MDC=∠MDP=
,∠MDC=∠MDP=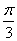 ,
,
所以AB与MD所成角的大小为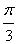 。
。
(3)解:∵AB∥平面OCD,
∴点A和点B到平面OCD的距离相等,
作AP⊥DC于P,
又OA⊥DC,
∴CD⊥平面OAP,CD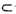 平面OCD,
平面OCD,
∴平面ODC⊥平面OAP,
又∵OP为平面OAP与平面OCD的交线,
在平面OAP内作AH⊥OP于H,
∴AH⊥平面OCD,
在Rt△OAP中, ,
,
∴点B到平面OCD的距离是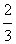 。
。


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
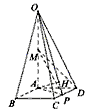
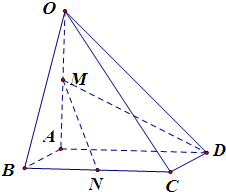 如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC中点,以A为原点,建立适当的空间直角坐标系,利用空间向量解答以下问题
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC中点,以A为原点,建立适当的空间直角坐标系,利用空间向量解答以下问题查看答案和解析>>
科目:高中数学 来源: 题型:
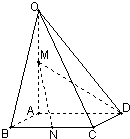 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=| π | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=| π | 4 |
查看答案和解析>>
科目:高中数学 来源:江苏同步题 题型:解答题
 ,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.
,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.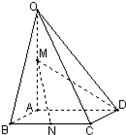
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com