
(本题满分12分)2014年国庆长假期间,各旅游景区人数发生“井喷”现象,给旅游区的管理提出了严峻的考验,国庆后,某旅游区管理部门对该区景点进一步改造升级,提高旅游增加值,经过市场调查,旅游增加值y万元与投入x万元之间满足: ,当x=10时,y=9.2.
,当x=10时,y=9.2.
(1)求y=f(x)的解析式;
(2)求旅游增加值y取得最大值时对应的x值.
(1)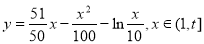 ;(2)当
;(2)当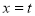 时,
时,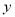 取得最大值.
取得最大值.
【解析】
试题分析:
(1)由题意可知,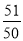 ×10-a×102-ln 1=9.2,从而求出
×10-a×102-ln 1=9.2,从而求出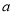 的值,代入确定
的值,代入确定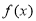 的解析式即可;
的解析式即可;
(2)求导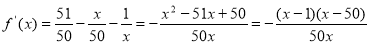 ,由导数确定函数的单调性即当x∈(1,50)时,
,由导数确定函数的单调性即当x∈(1,50)时,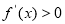 ,所以
,所以 在(1,50)上是增函数;当x∈(50,+∞)时,
在(1,50)上是增函数;当x∈(50,+∞)时,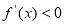 ,所以
,所以 在(50,+∞)上是减函数,从而求最值.
在(50,+∞)上是减函数,从而求最值.
试题解析:(1)因为当x=10时,y=9.2,即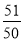 ×10-a×102-ln 1=9.2,解得a=
×10-a×102-ln 1=9.2,解得a=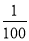 .
.
所以 .
.
(2)对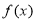 求导,得
求导,得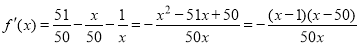 .
.
令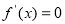 ,得
,得 或
或 (舍去).
(舍去).
当x∈(1,50)时,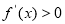 ,所以
,所以 在(1,50)上是增函数;
在(1,50)上是增函数;
当x∈(50,+∞)时,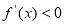 ,所以
,所以 在(50,+∞)上是减函数.
在(50,+∞)上是减函数.
所以当t>50时,当x∈(1,50)时,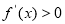 ,
, 在(1,50)上是增函数;当x∈(50,t]时,
在(1,50)上是增函数;当x∈(50,t]时,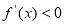 ,
, 在(50,t]上是减函数.∴当
在(50,t]上是减函数.∴当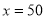 时,
时,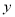 取得最大值;
取得最大值;
所以当t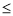 50时,当x∈(1,t)时,
50时,当x∈(1,t)时,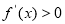 ,
, 在(1,t)上是增函数,所以当
在(1,t)上是增函数,所以当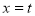 时,
时,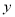 取得最大值.
取得最大值.
考点:利用导数求闭区间上函数的最值;函数解析式的求解及常用方法.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源:2015届湖北省襄阳市高三阶段性测试数学试卷(解析版) 题型:选择题
将4名同学录取到3所大学,每所大学至少要录取一名,则不同的录取方法共有( )
A.12 B.24 C.36 D.72
查看答案和解析>>
科目:高中数学 来源:2015届湖北省高三上学期期中考试理科数学试卷(解析版) 题型:选择题
对于非零复数 ,以下有四个命题
,以下有四个命题
①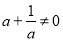
②
③若 ,则
,则 .
.
④若 则
则 .则一定为真的有( )
.则一定为真的有( )
A、②④ B、①③ C、①② D、③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com