
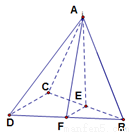
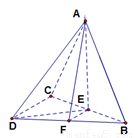
三棱锥 中,
中, 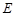 是
是 的中点,
的中点,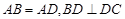
(I)求证: ;
;
(II)若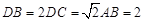 ,且二面角
,且二面角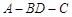 为
为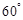 ,求
,求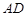 与面
与面 所成角的正弦值。
所成角的正弦值。
(I)见解析;(II)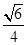 。
。
【解析】本试题主要是考查了立体几何总空间中的线线垂直的证明以及线面角的求解的综合运用。
(1)对于线线的垂直的证明,主要利用线面垂直的性质定理得到,先分先要证明的线和平面,然后找突破口进而求证。
(2)而对于线面角的求解问题,既可以采用向量法,也可以采用得到斜线和斜线在平面内的射影,借助于线面角的定义作出角,分析求解。
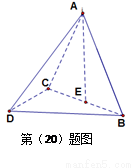
解:(I)如图取 的中点
的中点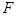 ,连
,连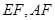 ,
,
∵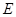 为
为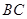 中点,
中点,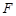 为
为 中点,∴
中点,∴ .
.
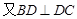 ∴
∴ .
.
∵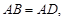 ∴
∴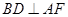
又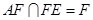 ,
,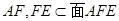
∴ …………4分
…………4分
∵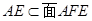 ,∴
,∴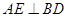 …………6分
…………6分
(II)由(I)知 ,
,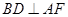
 。
。
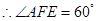 …………8分
…………8分

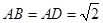 ,
,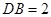
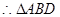 为等腰直角三角形,
为等腰直角三角形, ,
,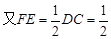

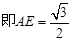
 …………10分
…………10分
又由(1)知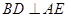
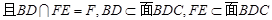
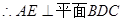
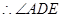 就是
就是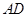 与面
与面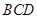 所成角
,
…………12分
所成角
,
…………12分
在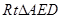 中,
中,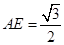 ,
,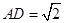
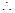
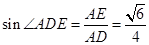 .
.
即直线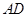 与面
与面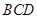 所成角的正弦值为
所成角的正弦值为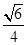 …………14分
…………14分


科目:高中数学 来源:2010-2011学年新疆乌鲁木齐八中高二下学期期末考试理科数学 题型:解答题
(9分)在三棱锥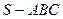 中,侧面
中,侧面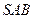 与侧面
与侧面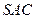 均是边长为
均是边长为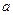 的正
的正
三角形, ,
, 是
是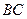 的中点,
的中点,
(1)求证: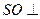 平面
平面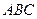 ;
;
(2)求二面角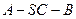 的余弦值
的余弦值
查看答案和解析>>
科目:高中数学 来源:2014届广东省高二上学期期末考试文科数学试卷(解析版) 题型:解答题
在三棱锥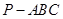 中,
中, 和
和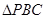 都是边长为
都是边长为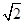 的等边三角形,
的等边三角形,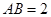 ,
,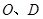 分别是
分别是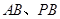 的中点.
的中点.
(1)求证: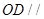 平面
平面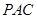 ;
;
(2)求证:平面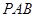 ⊥平面
⊥平面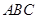 ;
;
(3)求三棱锥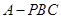 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com