练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知实数x，y满足（x+2）2+（y-3）2=1，则|3x+4y-26|的最小值为________．

    15
    分析：通过|3x+4y-26|的几何意义，利用圆心到直线的距离减去半径求解即可．
    解答：|3x+4y-26|的几何意义是圆上的点到直线3x+4y-26=0的距离减去半径后的5倍，
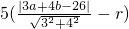
    （即：|3x+4y-26|=，（a，b）是圆心坐标，r是圆的半径．）
    就是所以实数x，y满足（x+2）2+（y-3）2=1，则|3x+4y-26|的最小值．
    圆的圆心坐标（-2，3），半径是1，
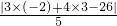
    所以圆心到直线的距离为：=4，
    所以|3x+4y-26|的最小值为5×（4-1）=15．
    故答案为：15．
    点评：本题考查简单线性规划的应用，考查点到直线的距离，转化思想的应用，考查计算能力．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知实数x，y满足
    x-y+2≥0
    x+y≥0
    x≤1
    ，则z=2x+y的最小值是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知实数x、y满足
    x≥1
    y≥2
    x+y≤4
    ，则u=
    x+y
    x
    的取值范围是
    [2，4]
    [2，4]
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知实数x，y满足
    x+y≤2
    x-y≤2
    0≤x≤1
    ，则z=2x-3y的最大值是
    6
    6
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知实数x，y满足
    y2-x≤0
    x+y≤2
    ，则2x+y的最小值为
    -
    1
    8
    -
    1
    8
    ，最大值为
    6
    6
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•安徽模拟）已知实数x，y满足|2x+y+1|≤|x+2y+2|，且|y|≤1，则z=2x+y的最大值为（　　）

    查看答案和解析>>

    同步练习册答案