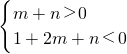C
分析:根据关于x的方程x
2+mx+m+n=0的两根分别为椭圆和双曲线的离心率,可得方程x
2+mx+m+n=0的两根,一根属于(0,1),另一根属于(1,+∞),从而可确定平面区域为D,进而利用函数y=log
a(x+3)(a>1)的图象上存在区域D上的点,可求实数a的取值范围.
解答:
解:构造函数f(x)=x
2+mx+m+n
∵关于x的方程x
2+mx+m+n=0的两根分别为椭圆和双曲线的离心率
∴方程x
2+mx+m+n=0的两根,一根属于(0,1),另一根属于(1,+∞)
∴
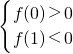
,∴
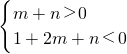
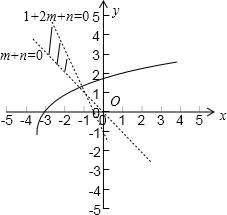
∵直线m+n=0,1+2m+n=0的交点坐标为(-1,1)
∴要使函数y=log
a(x+3)(a>1)的图象上存在区域D上的点,则必须满足1>log
a(-1+3)
∴log
a2<1
∵a>1
∴1<a<2
故选C.
点评:本题以方程根为载体,考查椭圆、双曲线的几何性质,考查数形结合的数学思想,确定平面区域是解题的关键.

 解:构造函数f(x)=x2+mx+m+n
解:构造函数f(x)=x2+mx+m+n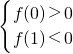 ,∴
,∴