
 如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和) 求二面角D-BC-A的大小;(结果用反三角函数值表示)
求二面角D-BC-A的大小;(结果用反三角函数值表示)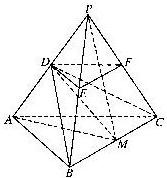 证明:(1)∵棱台DEF-ABC与棱锥P-ABC的棱长和相等,
证明:(1)∵棱台DEF-ABC与棱锥P-ABC的棱长和相等, ,由D是PA的中点,得
,由D是PA的中点,得 ,∴∠DMA=arcsin
,∴∠DMA=arcsin .
. ,底面相邻两边夹角为α,
,底面相邻两边夹角为α, sinα=V.
sinα=V.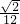 ,∴0<V<
,∴0<V<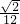 ,0<8V<1.可知α=arcsim(8V)
,0<8V<1.可知α=arcsim(8V) ,底面相邻两边夹角为arcsim(8V)的直平行六面体即满足要求.
,底面相邻两边夹角为arcsim(8V)的直平行六面体即满足要求. 取BC的中点M,连拉PM,DM.AM.说明∠DMA为二面角D-BC-A的平面角.
取BC的中点M,连拉PM,DM.AM.说明∠DMA为二面角D-BC-A的平面角. ,底面相邻两边夹角为α,
,底面相邻两边夹角为α, sinα=V.求出α=arcsim(8V)底面相邻两边夹角为arcsim(8V)的直平行六面体即满足要求
sinα=V.求出α=arcsim(8V)底面相邻两边夹角为arcsim(8V)的直平行六面体即满足要求

科目:高中数学 来源: 题型:
 如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:上海高考真题 题型:解答题

 PA,求二面角D-BC-A的大小;(结果用反三角函数值表示)
PA,求二面角D-BC-A的大小;(结果用反三角函数值表示)查看答案和解析>>
科目:高中数学 来源:2004年上海市高考数学试卷(文科)(解析版) 题型:解答题
 求二面角D-BC-A的大小;(结果用反三角函数值表示)
求二面角D-BC-A的大小;(结果用反三角函数值表示)
查看答案和解析>>
科目:高中数学 来源:2004年上海市高考数学试卷(理科)(解析版) 题型:解答题
 求二面角D-BC-A的大小;(结果用反三角函数值表示)
求二面角D-BC-A的大小;(结果用反三角函数值表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com