
(08年泉州一中适应性练习文)(12分)
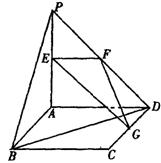
如图, PA⊥平面ABCD,ABCD为正方形, PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
(1)求证:PB∥面EFG;
(2)求异面直线EG与BD所成的角;
(3)求点A到平面EFG的距离。

解析:解法一:
(1)证明:取AB中点H,连结GH,HE,
∵E,F,G分别是线段PA、PD、CD的中点,
∴GH∥AD∥EF,
∴E,F,G,H四点共面. ……………………1分
又H为AB中点,
∴EH∥PB. ……………………………………2分
又EH![]() 面EFG,PB
面EFG,PB![]() 平面EFG,
平面EFG,
∴PB∥平面EFG. ………………………………4分
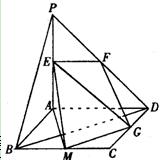
(2)解:取BC的中点M,连结GM、AM、EM,则GM//BD,
∴∠EGM(或其补角)就是异面直线EG与BD
所成的角.………………5分
在Rt△MAE中, ![]() ,
,
同理![]() ,…………………………6分
,…………………………6分
又![]() ,
,
∴在△MGE中,
![]() ………………7分
………………7分
故异面直线EG与BD所成的角为arccos![]() ,………………………………8分
,………………………………8分
解法二:建立如图所示的空间直角坐标系A-xyz,
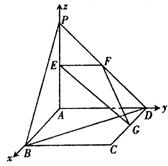
则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),
P(0,0,2),E(0,0,1),F(0,1,1),G(1,2,0).
(1)证明:![]()
![]() …………………………1分
…………………………1分
设![]() ,
,
即![]() ,
,

![]() ……………3分
……………3分
![]() ,
,
∴PB∥平面EFG. …………………………………………………………………… 4分
(2)解:∵![]() ,…………………………………………5分
,…………………………………………5分
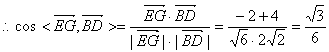 ,……………………… 7分
,……………………… 7分
故异面直线EG与BD所成的角为arccos![]() ,………………………………8分
,………………………………8分
(3) ![]()
![]() ,
,![]()
设面![]() 的法向量
的法向量![]()
则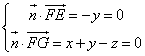
取法向量![]()
![]() A到平面EFG的距离
A到平面EFG的距离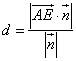 =
=![]() .…………………………12分
.…………………………12分


科目:高中数学 来源:不详 题型:填空题
| x1+x2 |
| 2 |
| x1x2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com