
设函数
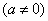 为奇函数,其图象在点
为奇函数,其图象在点 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数 的最小值为
的最小值为 .
.
(1)求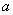 ,
, ,
, 的值;
的值;
(2)设 ,当
,当 时,求
时,求 的最小值.
的最小值.
科目:高中数学 来源: 题型:
如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中
的数学成绩.乙组记录中有一个数据模糊,无法确认,在图中以 表示.
表示.
已知甲、乙两个小组的数学成绩的平均分相同.
(1)求 的值;
的值;
(2)求甲、乙两个小组数学成绩的方差,并说明哪个小组的成绩相对比较稳定;

 参考公式:
参考公式:
查看答案和解析>>
科目:高中数学 来源: 题型:
下列结论中正确的是 ( )
A. 导数为零的点一定是极值点
B. 如果在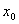 附近的左侧
附近的左侧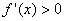 右侧
右侧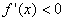 那么
那么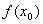 是极大值
是极大值
C. 如果在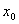 附近的左侧
附近的左侧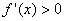 右侧
右侧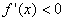 那么
那么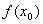 是极小值
是极小值
D. 如果在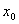 附近的左侧
附近的左侧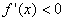 右侧
右侧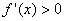 那么
那么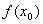 是极大值
是极大值
查看答案和解析>>
科目:高中数学 来源: 题型:
已知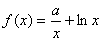 ,
, 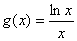 ,
,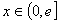 ,其中e是无理数且e=2.71828…,
,其中e是无理数且e=2.71828…,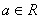 .
.
(1)若a=1,求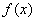 的单调区间与极值;
的单调区间与极值;
(2)求证:在(1)的条件下,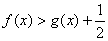 ;
;
(3)是否存在实数a,使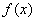 的最小值是-1?若存在,求出a的值;若不存在,说明理由.
的最小值是-1?若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com