
分析 (1)将a=3代入f(x),只需f(x)在某区间无解即可;(2)通过讨论a的范围,去掉绝对值结合不等式的解集求出a的值即可.
解答 解:(1)a=3时,f(x)=|x-5|-|x+a|=|x-5|-|x+3|,
若不等式f(x)≥k+2的解集不是R,
x≥5时,x-5-x-3≥k+2无解即可,即k>-10;
(2)若a≥-5,则-a<x<5时,
5-x-x-a≤1,解得:x≥$\frac{4-a}{2}$=$\frac{3}{2}$,解得:a=1,
若a<-5,则5<x<-a时,
x-5+x-a≤1,解得:x≤$\frac{6+a}{2}$,不合题意,
故a=1.
点评 本题考查了绝对值不等式问题,考查分类讨论思想,是一道中档题.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
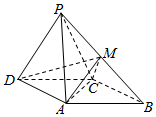 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,平面PDC⊥平面ABCD,AC=AD=PD=PC,∠DAC=90°,M在PB上.
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,平面PDC⊥平面ABCD,AC=AD=PD=PC,∠DAC=90°,M在PB上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3,4} | B. | {2,3} | C. | {1,2,3} | D. | {2,3,4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com