
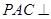 平面
平面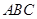 ,
,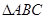 是以
是以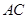 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,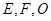 分别为
分别为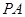 ,
,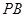 ,
,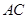 的中点,
的中点,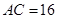 ,
,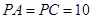 .
.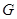 是
是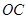 的中点,证明:
的中点,证明: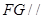 平面
平面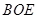 ;
;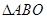 内是否存在一点
内是否存在一点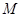 ,使
,使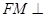 平面
平面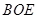 ,若存在,请找出点M,并求FM的长;若不存在,请说明理由。
,若存在,请找出点M,并求FM的长;若不存在,请说明理由。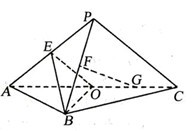
 。
。 ,
, ,
,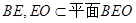 ,
,
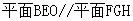 ,∵
,∵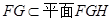 ,∴
,∴ 。 …………5分
。 …………5分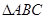 是以
是以 为斜边的等腰直角三角形,且O为AC中点,∴
为斜边的等腰直角三角形,且O为AC中点,∴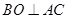 ,
,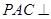 平面
平面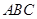 ,
,  ,
, ,
,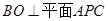 。
。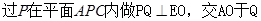 ,所以
,所以 ,
, ,∴
,∴ ,
, ,连结FM,因为点F为PB中点,
,连结FM,因为点F为PB中点, ,进而
,进而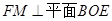 ,
, 。
。 …………12分
…………12分

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
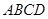 和矩形
和矩形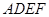 所在平面相互垂直,
所在平面相互垂直,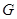 是
是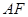 的中点.
的中点. 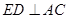 ;
;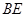 与平面
与平面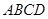 成45o角,求异面直线
成45o角,求异面直线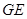 与
与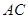 所成角的余弦值.
所成角的余弦值.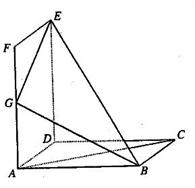
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
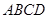 中,
中,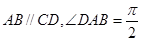 ,点
,点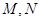 分别在
分别在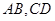 上,且
上,且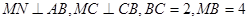 ,现将梯形
,现将梯形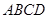 A沿
A沿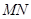 折起,使平面
折起,使平面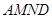 与平面
与平面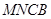 垂直(如图②).
垂直(如图②).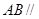 平面
平面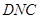 ;
; 时,求二面角
时,求二面角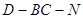 的大小.
的大小.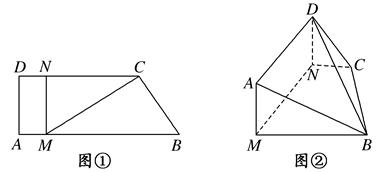
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.若直线 、 、 互相平行,则直线 互相平行,则直线 、 、 确定一个平面 确定一个平面 |
| B.若四点不共面,则这四点中任意三点都不共线 |
| C.若两条直线没有公共点,则这两条直线是异面直线 |
| D.两条异面直线不可能垂直于同一个平面 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
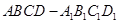 的面对角线
的面对角线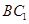 上运动,则下列四个命题:①三棱锥
上运动,则下列四个命题:①三棱锥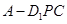 的体积不变; ②
的体积不变; ②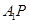 ∥面
∥面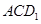 ; ③
; ③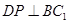 ; ④面
; ④面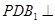 面
面 。其中正确的命题的序号是_______________(写出所有你认为正确结论的序号)
。其中正确的命题的序号是_______________(写出所有你认为正确结论的序号)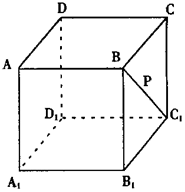
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com