
 如图,M,N,K分别是正方体ABCD-A1B1C1D1的棱AB,CD,C1D1的中点.
如图,M,N,K分别是正方体ABCD-A1B1C1D1的棱AB,CD,C1D1的中点.
|


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
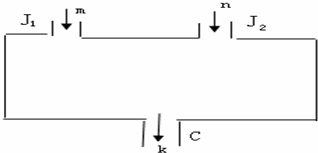 21、如图所示,一个计算装置示意图.J1、J2是数据入口,C 是计算结果的出口.计算过程是:由J1、J2 分别输入自然数m和n,经过计算所得结果由出口C输出k,即:f(m,n)=k.此种计算装置满足以下三个性质:①f(1,1)=1;②f(m,n+1)=f(m,n)+2;③f(m+1,1)=2f(m,1).
21、如图所示,一个计算装置示意图.J1、J2是数据入口,C 是计算结果的出口.计算过程是:由J1、J2 分别输入自然数m和n,经过计算所得结果由出口C输出k,即:f(m,n)=k.此种计算装置满足以下三个性质:①f(1,1)=1;②f(m,n+1)=f(m,n)+2;③f(m+1,1)=2f(m,1).查看答案和解析>>
科目:高中数学 来源: 题型:
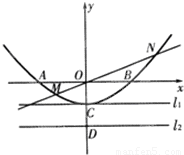
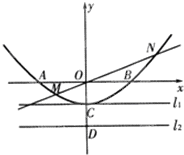 如图,已知抛物线与坐标轴分别交于A(-2,0)、B(2,0)、C(0,-1)三点,过坐标原点O的直线y=kx与抛物线交于M、N两点.分别过点C、D(0,-2)、作平行于x轴的直线
如图,已知抛物线与坐标轴分别交于A(-2,0)、B(2,0)、C(0,-1)三点,过坐标原点O的直线y=kx与抛物线交于M、N两点.分别过点C、D(0,-2)、作平行于x轴的直线查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,这是一个计算机装置示意图,A、B是数据入口处,C是计算机结果的出口,计算过程是由A、B分别输入自然数m和n,经过计算后,得自然数k,由C输出.即:f(m,n)=k,此种计算装置完成计算,满足以下三个性质:①若A、B分别输入1,则输出结果为1,即f(1,1)=1;②若A输入自然数m,B输入自然数由n变为n+1,则输出结果比原来增大2,即f(m,n+1)=f(m,n)+2;③若B输入1,A输入自然数由m变为m+1,则输出结果是原来的2倍,即f(m+1,1)=2f(m,1).
如图,这是一个计算机装置示意图,A、B是数据入口处,C是计算机结果的出口,计算过程是由A、B分别输入自然数m和n,经过计算后,得自然数k,由C输出.即:f(m,n)=k,此种计算装置完成计算,满足以下三个性质:①若A、B分别输入1,则输出结果为1,即f(1,1)=1;②若A输入自然数m,B输入自然数由n变为n+1,则输出结果比原来增大2,即f(m,n+1)=f(m,n)+2;③若B输入1,A输入自然数由m变为m+1,则输出结果是原来的2倍,即f(m+1,1)=2f(m,1).查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 | 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省九江市示范性高中高一(上)10月月考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com