
对于在区间[m,n]上有意义的两个函数f(x)与g(x),如果对于任意![]() ,均有|f(x)-g(x)|≤1,则称f(x)与g(x)在[m,n]上是接近的.若函数y=x2-2x+3与函数y=3x-2在区间[m,n]上是接近的,给出如下区间①[1,4];②[1,3];③[1,2]∪[3,4];④
,均有|f(x)-g(x)|≤1,则称f(x)与g(x)在[m,n]上是接近的.若函数y=x2-2x+3与函数y=3x-2在区间[m,n]上是接近的,给出如下区间①[1,4];②[1,3];③[1,2]∪[3,4];④![]() .则区间[m,n]可以是________.(把你认为正确的序号都填上)
.则区间[m,n]可以是________.(把你认为正确的序号都填上)
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 3 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | x-a |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分)对于在区间[m,n]上有意义的两个函数![]() 与
与![]() ,如果对任意
,如果对任意![]() [m,n]均有
[m,n]均有![]() ,称
,称![]() 与
与![]() 在[m,n]上是接近的,否则称
在[m,n]上是接近的,否则称![]() 与
与![]() 在[m,n]上是非接近的,现有两个函数
在[m,n]上是非接近的,现有两个函数![]() 与
与![]() (a>0,a≠1),给定区间[a+2,a+3].(1)若
(a>0,a≠1),给定区间[a+2,a+3].(1)若![]() 与
与![]() 在给定区间[a+2,a+3]上都有意义,求a的取值范围;(2)讨论
在给定区间[a+2,a+3]上都有意义,求a的取值范围;(2)讨论![]() 与
与![]() 在[a+2,a+3]上是否是接近的.
在[a+2,a+3]上是否是接近的.
查看答案和解析>>
科目:高中数学 来源:2014届安徽省高二下学期期末考试数学试卷(解析版) 题型:解答题
对于在区间 [ m,n ] 上有意义的两个函数 与
与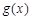 ,如果对任意
,如果对任意 ,均有
,均有 ,则称
,则称 与
与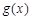 在 [ m,n ] 上是友好的,否则称
在 [ m,n ] 上是友好的,否则称 与
与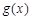 在 [ m,n ]是不友好的.现有两个函数
在 [ m,n ]是不友好的.现有两个函数 与
与 (a > 0且
(a > 0且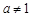 ),给定区间
),给定区间 .
.
(1)若 与
与 在给定区间
在给定区间 上都有意义,求a的取值范围;
上都有意义,求a的取值范围;
(2)讨论 与
与 在给定区间
在给定区间 上是否友好.
上是否友好.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com