
 的两焦点分别为F1和F2,若双曲线上存在不是顶点的点P,使得∠PF2F1=3∠PF1F2,则双曲线离心率e的取值范围是________.
的两焦点分别为F1和F2,若双曲线上存在不是顶点的点P,使得∠PF2F1=3∠PF1F2,则双曲线离心率e的取值范围是________.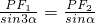 ,利用三倍角公式化简得PF1=(3-4sin2α)PF2,再利用双曲线的定义,可得PF2=
,利用三倍角公式化简得PF1=(3-4sin2α)PF2,再利用双曲线的定义,可得PF2=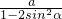 ,最后根据P在双曲线右友,可得关于e的不等式,进而根据三角函数的范围确定e的范围.
,最后根据P在双曲线右友,可得关于e的不等式,进而根据三角函数的范围确定e的范围.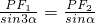 ,
,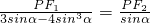
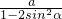 ,
,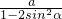 >c-a,∴
>c-a,∴ <1+
<1+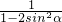 ≤2,
≤2, <2,又
<2,又 >1,
>1,

科目:高中数学 来源: 题型:
| 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 | 4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 5 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2006-2007学年江苏省宿迁市高二(上)期末数学模拟试卷2(文科)(解析版) 题型:解答题
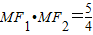 ,
,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com