
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 根据余弦定理,算出(b+c)2=4+3bc,再利用基本不等式bc≤[$\frac{1}{2}$(b+c)]2,加以计算,可得b+c≤4,即可得到△ABC周长的最大值.
解答 解:∵在△ABC中,A=60°,a=2,
∴由余弦定理,得a2=b2+c2-2bccosA,
即4=b2+c2-2bccos60°,化简得(b+c)2=4+3bc,
∵bc≤[$\frac{1}{2}$(b+c)]2,
∴(b+c)2≤4+$\frac{3}{4}$(b+c)2,解得(b+c)2≤16,
由此可得b+c≤4,△ABC周长AB+AC+BC≤6.
即当且仅当b=c=2时,△ABC周长的最大值为6.
故选:C.
点评 本题给出三角形的一边和它的对角,求周长的最大值.着重考查了用余弦定理解三角形和基本不等式求最值等知识,属于中档题.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:解答题
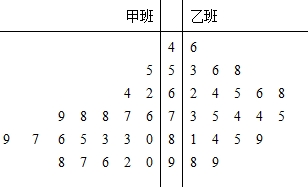
| 学业成绩 | 低于70分 | 70分到89分 | 不低于90分 |
| 学业水平 | 一般 | 良好 | 优秀 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,$\frac{5}{4}$] | B. | [$\frac{1}{2}$,$\frac{3}{4}$] | C. | (0,$\frac{1}{2}$] | D. | (0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com