练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

     设函数。

       （1）若函数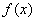是定义域上的单调函数，求实数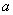的取值范围；

       （2）求函数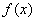的极值点。

     

     

     

     

     

     

    【答案】

     【解析】（1），若函数是定义域上的单调函数，则只能在上恒成立，即在上恒成立恒成立，令，则函数图象的对称轴方程是，故只要恒成立，即只要。

    （2）有（1）知当时，的点是导数不变号的点，

    故时，函数无极值点；

    当时，的根是，

    若，，此时，，且在上，

    在上，故函数有唯一的极小值点；（7分）

    当时，，此时，

    在都大于，在上小于 ，

    此时有一个极大值点和一个极小值点．

    综上可知，时，在上有唯一的极小值点；

    时，有一个极大值点和一个极小值点；

    时，函数在上无极值点。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    对实数a与b，定义新运算“?”：a?b=
    a，a-b≤1
    b，a-b＞1
    ．设函数f（x）=（x2-2）?（x-1），x∈R．若函数y=f（x）-c的图象与x轴恰有两个公共点，则实数c的取值范围是（　　）
    A、（-1，1]∪（2，+∞）
    B、（-2，-1]∪（1，2]
    C、（-∞，-2）∪（1，2]
    D、[-2，-1]

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年河北省邯郸市高三9月月考文科数学试卷（解析版） 题型：解答题

    设函数。

       （1）若函数是定义域上的单调函数，求实数的取值范围；

       （2）求函数的极值点。

     

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年度新课标高三下学期数学单元测试4-理科 题型：解答题

     

        设函数

       （1） 求函数；

       （2） 若存在常数k和b,使得函数对其定义域内的任意实数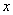分别满足则称直线的“隔离直线”．试问:函数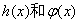是否存在“隔离直线”?若存在,求出“隔离直线”方程,不存在,请说明理由．

     

     

     

     

     

     

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年度新课标高三下学期数学单元测试3-理科 题型：解答题

     

        已知函数f（x）对任意的实数x、y都有f（x+y） =f（x）+f（y）-1，且当x>0 时，

    f（x）＞1．

       （1）求证：函数f（x）在R上是增函数；

       （2）若关于x的不等式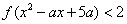的解集为{x|-3＜x＜2＝，求f（2009）的值；

       （3）在（2）的条件下，设,若数列从第k项开始的连续20项之和等于102，求k的值．

     

     

     

     

     

     

     

    查看答案和解析>>

    同步练习册答案