
已知函数f(x)对任意的实数x、y都有f(x+y) =f(x)+f(y)-1,且当x>0 时,
f(x)>1.
(1)求证:函数f(x)在R上是增函数;
(2)若关于x的不等式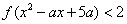 的解集为{x|-3<x<2=,求f(2009)的值;
的解集为{x|-3<x<2=,求f(2009)的值;
(3)在(2)的条件下,设 ,若数列
,若数列 从第k项开始的连续20项之和等于102,求k的值.
从第k项开始的连续20项之和等于102,求k的值.
(1)证明:设x1>x2,则x1-x2>0,从而f(x1-x2)>1,即f(x1-x2)-1>0.………2分
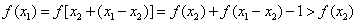 ,
,
故f(x)在R上是增函数.…4分
(2)设2 =f(b),于是不等式为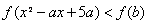 .
.
则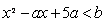 ,即
,即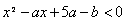 .………6分
.………6分
∵不等式f(x2 -ax +5a) <2的解集为{x|-3<x<2},
∴方程x2-ax+5a-b=0的两根为-3和2,
于是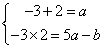 ,解得
,解得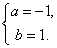 ∴f(1)=2.………8分
∴f(1)=2.………8分
在已知等式中令x=n,y=1,得f(n+1)-f(n) =1.
所以{f(n)}是首项为2,公差为1的等差数列.
f(n)=2+(n-1)×1=n+1,故f(2009)=2010.………10分
(3)
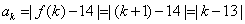 .
.
设从第k项开始的连续20项之和为Tk,则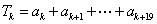 .
.
当k≥13时,ak=|k-13|=k-13,Tk≥T13=0+1+2+3+…+19=190>102. (11分)
当k<13时,ak=|k-13|=13-k.
Tk=(13-k)+(12一k)+…+1+0+1+…+(k+6)=k2一7k+112.
令kk+112=102,解得k=2或k=5.………14分
(注:当k≥13时,ak=|k一13|=k一13,令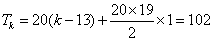 ,
,
无正整数解.得11分)


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| ab |
| kπ |
| 2 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ab |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ex |
| ex+1 |
| 1 |
| 2 |
| x+1 |
| x+2 |
| 1 |
| 4 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com