设函数f(x)=ax2+bx+1(a,b∈R),
(1)若f(-1)=0且对任意实数x均有f(x)≥0成立,求f(x)表达式;
(2)在(1)的条件下,g(x)=f(x)-16x(x∈[m,10],其中常数m>0),区间D为g(x)的值域,若D的长度为23-2m,求此时m的值.
【答案】
分析:(1)由f(-1)=0,知b=a=1,由f(x)≥0恒成立,知a>0,且△=(a-1)
2≤0,由此能求出f(x).
(2)由题设知g(x)=x
2-14x+1,23-2m=g(x)
max-g(x)
min,由此进行分类讨论,能求出m的值.
解答:(本题12分)
解:(1)∵f(-1)=0,∴b=a=1,
由f(x)≥0恒成立,知a>0,且△=b
2-4a=(a+1)
2-4a=(a-1)
2≤0,
∴a=1.
∴f(x)=x
2+2x+1.(3分)
(2)∵g(x)=f(x)-16x(x∈[m,10],其中常数m>0),区间D为g(x)的值域,
D的长度为23-2m,
∴g(x)=x
2-14x+1,23-2m=g(x)
max-g(x)
min,(5分)
①当m∈[7,10)时,23-2m=g(10)-g(t)=-m
2+16m,得:m=7或9.(7分)
②当m∈[4,7)时,23-2m=g(10)-g(7),得m=7(舍).(9分)
③当m∈(0,4)时,23-2m=g(m)-g(7),m
2-12m+26=0,
解得:m=
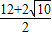
(舍)或m=
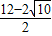
=6-
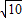
.(11分)
综合得m=6-
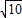
,或m=7,或m=9.(12分)
点评:本题考查函数的解析式的求法,考查满足条件的实数值.解题时要认真审题,注意配方法、等价转化思想、分类讨论思想的合理运用.

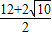 (舍)或m=
(舍)或m=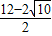 =6-
=6-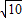 .(11分)
.(11分)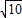 ,或m=7,或m=9.(12分)
,或m=7,或m=9.(12分)

 名校课堂系列答案
名校课堂系列答案 设函数f(x)=(a
设函数f(x)=(a