
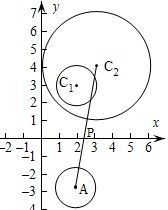 解:如图,圆C1关于x轴的对称圆的圆心坐标A(2,-3),半径为1,圆C2的圆心坐标(3,4),半径为3,
解:如图,圆C1关于x轴的对称圆的圆心坐标A(2,-3),半径为1,圆C2的圆心坐标(3,4),半径为3,| (3-2)2+(4+3)2 |
| 2 |
| 2 |


科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、4,2 | B、5,3 |
| C、5,2 | D、6,2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 食品 | 衣着 | 家庭设备用品及服务 | 医疗保健 | 交通和通讯 | 教育文化娱乐服务 | 居住 | 杂项商品和服务 |
| 39.4% | 5.9% | 6.2% | 7.0% | 10.7% | 15.9% | 11.4% | 3.5% |
| A、条形统计图 | B、茎叶图 |
| C、扇形统计图 | D、折线统计图 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com