
如图,底面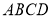 是边长为2的菱形,且
是边长为2的菱形,且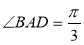 ,以
,以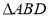 与
与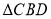 为底面分别作相同的正三棱锥
为底面分别作相同的正三棱锥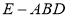 与
与 ,且
,且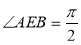 .
.

(1)求证: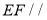 平面
平面 ;
;
(2)求平面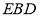 与平面
与平面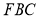 所成锐角二面角的余弦值.
所成锐角二面角的余弦值.
(1)证明过程见解析;(2)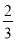 .
.
【解析】
试题分析:(1)作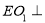 面
面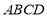 于
于 ,作
,作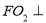 面
面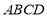 于
于 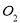 ,易得四边形
,易得四边形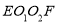 是平行四边形,所以
是平行四边形,所以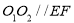 .又
.又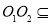 面
面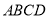 ,
,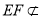 面
面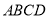 ,所以
,所以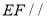 平面
平面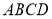 ;
;
(2)以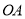 为
为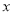 轴的正方向,以
轴的正方向,以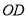 为
为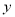 轴的正方向,在平面
轴的正方向,在平面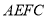 中过
中过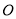 点作面
点作面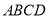 的垂线为
的垂线为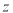 轴,建立空间直角坐标系求题,利用向量,求出平面
轴,建立空间直角坐标系求题,利用向量,求出平面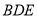 和平面
和平面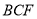 的法向量,则两平面的法向量的夹角即为所求角或为所求角的补角.
的法向量,则两平面的法向量的夹角即为所求角或为所求角的补角.
(1)作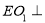 面
面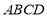 于
于 ,作
,作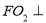 面
面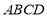 于
于 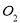 ,因
,因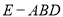 与
与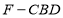 都是正三棱锥, 且
都是正三棱锥, 且 、
、 分别为
分别为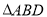 与
与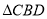 的中心,
的中心,

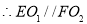 且
且 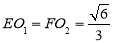 .
.
所以四边形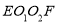 是平行四边形,所以
是平行四边形,所以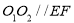 .
.
又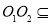 面
面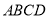 ,
,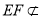 面
面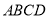 ,所以
,所以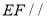 平面
平面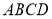
(2)如图,建立空间直角坐标系,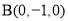 、
、 、
、 、
、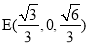 、
、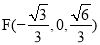 .
.

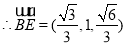 、
、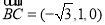 、
、
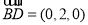 、
、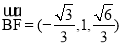 .…7分
.…7分
设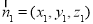 为平面
为平面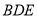 的法向量,
的法向量,
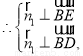



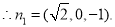
设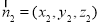 为平面
为平面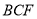 的法向量,
的法向量,
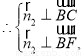



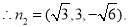
设平面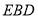 与平面
与平面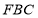 所成锐二面角为
所成锐二面角为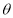 ,
,
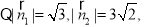
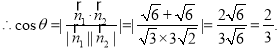
所以,面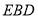 与面
与面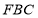 所成锐二面角的余弦值为
所成锐二面角的余弦值为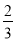 .
.
考点:线面平行的判定;二面角的求解.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源:2013-2014学年山东省东营市高三4月统一质量检测考试理科数学试卷(解析版) 题型:选择题
已知 ,函数
,函数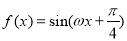 在
在 上单调递减.则
上单调递减.则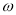 的取值范围是 ( )
的取值范围是 ( )
A.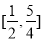 B.
B.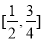 C.
C.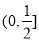 D.
D.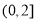
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省东营市高三4月统一质量检测考试文科数学试卷(解析版) 题型:选择题
已知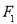 ,
,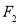 是双曲线
是双曲线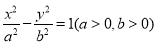 的左,右焦点,若双曲线左支上存在一点
的左,右焦点,若双曲线左支上存在一点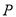 与点
与点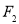 关于直线
关于直线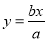 对称,则该双曲线的离心率为( )
对称,则该双曲线的离心率为( )
A.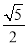 B.
B.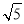 C.
C.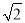 D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省东营市高三4月统一质量检测考试文科数学试卷(解析版) 题型:选择题
已知 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最大值为 ( )
的最大值为 ( )
A.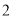 B.
B. C.
C.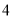 D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省皖北协作区高三年级联考理科数学试卷(解析版) 题型:填空题
3个单位从4名大学毕业生中选聘工作人员,若每个单位至少选聘1人(4名大学毕业生不一定都能选聘上),则不同的选聘方法种数为________(用具体数字作答)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省皖北协作区高三年级联考文科数学试卷(解析版) 题型:填空题
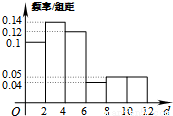
某公司为改善职工的出行条件,随机抽取50名职工,调查他们的居住地与公司的距离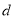 [单位:千米].若样本数据分组为
[单位:千米].若样本数据分组为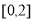 ,
, 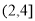 ,
,  ,
, 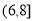 ,
, 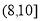 ,
, 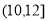 , 有数据绘制的频率分布直方图如图所示,则样本中职工居住地与公司的距离不超过4千米的人数为__________.
, 有数据绘制的频率分布直方图如图所示,则样本中职工居住地与公司的距离不超过4千米的人数为__________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省安庆市高三第二次模拟考试文科数学试卷(解析版) 题型:填空题
已知点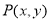 满足约束条件
满足约束条件 ,
, 为坐标原点,则
为坐标原点,则 的最大值为_______________.
的最大值为_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com