已知集合A={x|x2+a≤(a+1)x,a∈R}.
(Ⅰ)求A;
(Ⅱ)若a>0,以a为首项,a为公比的等比数列前n项和记为Sn,对于任意的n∈N+,均有Sn∈A,求a的取值范围.
解:(Ⅰ)A={x|x
2+a≤(a+1)x,a∈R}={x|(x-1)(x-a)≤0,a∈R}.
(1)a≥1时,A={x|1≤x≤a};
(2)a<1时,A={x|a≤x≤1}
(Ⅱ)(i)当a≥1时,A={x|1≤x≤a}.
而S
2=a+a
2>a,S
2∉A,故a≥1时,不存在满足条件的a;
(ii)当0<a<1时,A={a≤x≤1},
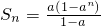
,
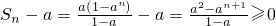
,∴S
n≥a,
又a
n>0,∴
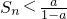
对任意的n∈N
+,S
n∈A,只须a满足
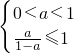
,解得
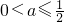
.
综上所述,a的取值范围是
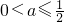
.
分析:(Ⅰ)解含参数的不等式,把不等式x
2+a≤(a+1)x化成标准形式,因式分解求得相应方程的根,比较根的大小,从而确定不等式的解集;(Ⅱ)求a为公比的等比数列前n项和记为S
n,对公比a是否为1讨论,求出S
n,根据对于任意的n∈N
+,均有S
n∈A,解不等式,求得a的取值范围.
点评:解含参数的不等式,根的大小是确定分类标准的一种方法,等比数列求和,一定对公比q是否为零进行讨论,体现了分类讨论的数学思想,属中档题.

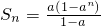 ,
,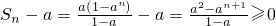 ,∴Sn≥a,
,∴Sn≥a,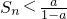
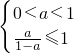 ,解得
,解得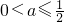 .
.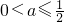 .
.

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案