
已知角A、B、C为△ABC的三个内角,其对边分别为a、b、c,若=(-cos,sin),=(cos,sin),a=2,且·=.
(1)若△ABC的面积S=,求b+c的值.
(2)求b+c的取值范围.
(1)4;(2)?2,4?
【解析】
试题分析:(1)由=(-cos,sin),=(cos,sin),且·=.可求得角A的值,又因为△ABC的面积S=,a=2,在三角形中利用余弦与三角形的面积公式,即可解出b,c的值或者直接构造b+c,即可得到结论.
(2)由(1)可知角A,以及边长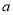 .用角B结合正弦定理分别表示出b,c.再结合角B的范围,求出b+c的取值范围即可.
.用角B结合正弦定理分别表示出b,c.再结合角B的范围,求出b+c的取值范围即可.
试题解析:(1)∵=(-cos,sin),=(cos,sin),且·=,
∴-cos2+sin2=,即-cosA=,
又A∈(0,π),∴A=. 3分
又由S△ABC=bcsinA=,所以bc=4,
由余弦定理得:a2=b2+c2-2bc·cos=b2+c2+bc,
∴16=(b+c)2,故b+c=4. 7分
(2)由正弦定理得:====4,又B+C=?-A=,
∴b+c=4sinB+4sinC=4sinB+4sin(-B)=4sin(B+), . 12分
∵0<B<,则<B+<,则<sin(B+)≤1,即b+c的取值范围是?2,4? ..14分
考点:1.三角函数恒等变换.2.正余弦定理的应用.3.三角函数最值的求法.


科目:高中数学 来源:2013-2014学年湖北省黄冈市高三第二学期三月月考文科数学试卷(解析版) 题型:填空题
设x,y满足 若目标函数z=ax+y(a>0)的最大值为14,则a=
若目标函数z=ax+y(a>0)的最大值为14,则a=
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省黄冈市高三第二学期三月月考文科数学试卷(解析版) 题型:选择题
如图,等边三角形 的中线
的中线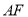 与中位线
与中位线 相交于
相交于 ,已知
,已知 是△
是△ 绕
绕 旋转过程中的一个图形,下列命题中,错误的是( )
旋转过程中的一个图形,下列命题中,错误的是( )

A.动点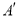 在平面
在平面 上的射影在线段
上的射影在线段 上
上
B.恒有平面 ⊥平面
⊥平面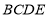
C.三棱锥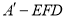 的体积有最大值
的体积有最大值
D.异面直线 与
与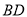 不可能垂直
不可能垂直
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省武汉市高三下学期4月调研测试理科数学试卷(解析版) 题型:选择题
设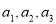 均为正数,
均为正数,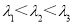 ,则函数
,则函数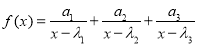 的两个零点分别位于区间( )
的两个零点分别位于区间( )
A.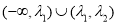 内 B.
内 B.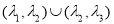 内
内
C. 内 D.
内 D. 内
内
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com